 |


航技研数値風洞(NWT)を用いた格子ボルツマン法の大規模計算
東京大学大学院
鈴木宏二郎、今村太郎
1.はじめに
格子ボルツマン法を用いた非圧縮流計算が,差分法等と同様に有効な計算法であることが,近年示されてきた。この方法は非圧縮ナヴィエストークス方程式の差分法解析で必要となる圧力の反復計算がないなどの特徴を持ち,アルゴリズムが単純で,並列計算に適している。しかしながら,等間隔直交格子のような等方的な計算格子上で定式化されており,境界条件の設定に柔軟性を欠くなど,実用問題への適用には課題が残っていた。そこで,我々は格子ボルツマン法を一般座標系に拡張する新しい手法を提案し,同時に物体適合座標系に適した境界条件を導出した。本手法を用いれば,差分法と同様に構造格子を作成し,任意の物体周りの流れを解析できる。更に本計算手法をベクトルパラレル計算機であるNWT用に並列化した。
2.NWTによる並列化
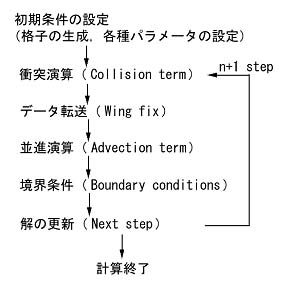
図1は一般座標系に拡張した格子ボルツマン法(Generalized Interpolation-based Lattice Boltzmann Method:GILBM)のNWT上での計算アルゴリズムを示す。格子ボルツマン法では流体を粒子の衝突と並進でモデル化する。GILBMでは演算の9割以上を粒子の並進演算が占めるので,全体の並列化効率を高めるためには,並進演算を高効率に並列化する必要がある。図2は,横軸にPE数,縦軸に計算時間をとり,図1で示した関数毎に要する計算時間をまとめたものである。並進演算が効率的に並列化されており,Totalの計算時間もPE数の増加にほぼ反比例して減少している。またPE数が増加してもWingFix(PE間のデータ転送)に要する時間が大幅には増加しない点も,大きな長所であると考えられる。NWTで並列化したことにより,複雑形状や高レイノルズ数流れなど格子点数の大きい大規模な格子ボルツマン法の計算が可能になった。
|
 |
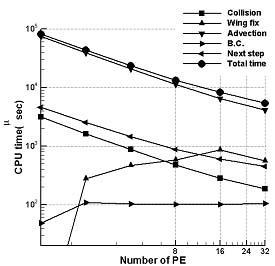 |
図1 GILBMにおける計算手順 |
図2 GILBMによる並列計算 |
|
3.NWTによるGILBMの計算例
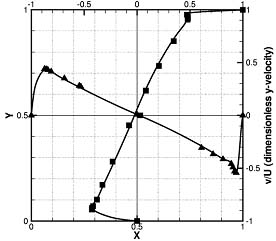
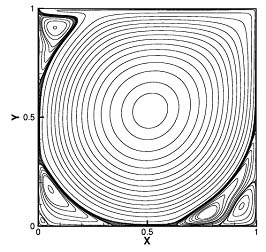
以下にGILBMを用いた計算例を示す。図3は2次元キャビティ問題(レイノルズ数104)の計算結果である。この問題はしばしば非圧縮計算コードのベンチマーク問題として扱われる。発生する渦の数,渦の位置,および強さを差分法で計算されたものと比較したところ,十分な精度で一致した。
|
|
|
Symbol:Ghia(差分解),Line: GILBM
Ghiaの計算結果との比較 |
流線分布 |
|
図3:Re=104におけるCavity Flow
|
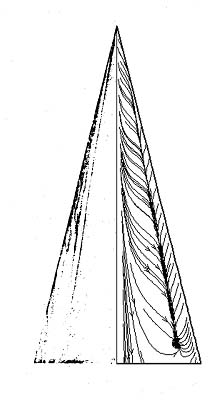
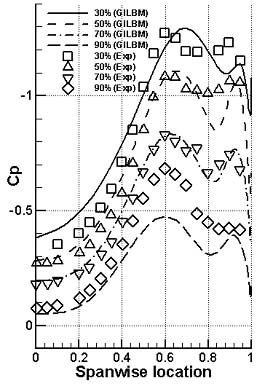
図4左はデルタ翼(アスペクト比1,レイノルズ数9×105,迎角20.5°)の計算例である。デルタ翼表面近傍の流線分布から,二次剥離が捕らえられていることが確認できた。また表面圧力分布(図4右)も実験結果と定性的に一致した。
|
 |
|
実験結果
|
計算結果:表面圧力分布(上面側)
|
|
図4:デルタ翼の計算例(Re=9×105, AOA=20.5°
|
4.より大規模な計算について
航空機全機まわりの計算には1000万点程度の格子点が必要となる。GILBMで必要となるメモリから,26PE以上で計算が可能である。また,106step(収束するまで)に要する計算時間は,およそ600時間である。LBMを一般座標系に拡張したことで,NWTを用いた実用的な計算が可能になった。
5.まとめ
一般座標系に拡張した格子ボルツマン法をNWT用に並列化した結果,並列化効率の高い,非圧縮流体ソルバーを構築することができた。今後は,従来の流体計算コードとの比較を行ない,本手法の長所短所を明確にする予定である。
参考文献
- T.Imamura, K.Suzuki, T.Nakamura, M.Yoshida, M.Fukuda;The Application of Lattice
Boltzmann Method to the Large Scale Flow Computation(in Japanese), NAL SP 53,2002.1,pp.203〜208
- T.Imamura, K.Suzuki, T.Nakamura, M.Yoshida, M.Fukuda;Large
scale flow simulation using generalized coordinate lattice Boltzmann method,
High Performance Computing Symposium 2002. pp.113〜118
|
|



