 |


ヘリコプタのブレード/渦干渉騒音について
航空宇宙技術研究所
青山剛史、近藤夏樹、齊藤茂
1.はじめに
垂直に離着陸し空中に静止できるヘリコプタは、その高機動性故、山地が多く国土の狭い我が国の国土事情に適合しているため、消防・防災や、警察及び海上保安庁などによる公共活動のみならず、薬剤散布、建設資材輸送、送電線巡視、報道取材等、国民生活に密着した様々な分野で活用されている。その結果、我が国は世界第3位のヘリコプタ保有大国となっており、民間の航空機登録機数におけるヘリコプタの割合は世界的にも他に例を見ない3割にも上っている。しかし、主に安全性と騒音の問題がそのさらなる普及を妨げる要因となっている。
本報告のテーマである騒音問題について言えば、現状のヘリコプタの運航においては、離着陸時に人家を迂回したり、土日や早朝、昼休みの飛行を避けるなど、住民の騒音被害に配慮した限定的飛行をせざるを得ない状況であるが、騒音の問題を解決すれば運航の自由度が増し、居住地域に近接する場所での交通手段として、ヘリコプタの利用を促進することができる。また、ヘリコプタによる救急搬送が普及している欧米では、騒音による事業の制限の問題が顕在化しているが、ドクターヘリの普及に伴って我が国でも生じると予測されるこの問題を、低騒音化によって解決することができる。
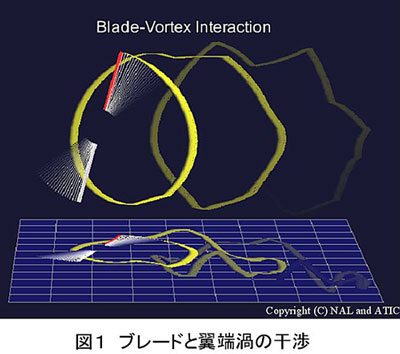
ヘリコプタの騒音には様々なものがあるが、中でもメイン・ロータのブレードと翼端渦が干渉する時に起こるブレード/渦干渉(BVI: Blade-Vortex Interaction)騒音は、バタバタと聞こえる極めて耳障りなものである。この騒音は、図1のようにメイン・ロータのブレードが、先行する他のブレードもしくは自身の放出した翼端渦を切ったり、その近くを通過する時に、ブレードの空力荷重が急激に変動することによって生ずる。発生条件は機体によって異なるが、一般的に低速降下中や急旋回時に発生しやすく、前進方向の下方に強く伝播するので、ヘリコプタが着陸する際、付近の住民に与える影響が大きく、都市部におけるヘリポート設置の妨げとなっている。
航空宇宙技術研究所では(株)コミュータヘリコプタ先進技術研究所(ATIC)との共同研究の下、2つの騒音解析法を開発し、NWTを最大限に活用することによって、BVI騒音の発生メカニズム解明とその低減法に関する研究を行った。以下にその結果を報告する。
|
|
2.解析法
2.1 組み合せ解析法[1]
本解析法は4段階からなっている。まず1段階目は、ヘリコプタ全体にかかる力の平衡状態を求め、ブレードと翼端渦の位置関係を算出するトリム解析である。この段階では計算時間と収束性の限界から、方位角方向に10°刻みの計算を行っている。しかし、ブレードと翼端渦の干渉は瞬時の現象なので、この刻み幅では精度不足である。そこで、2段階目においてブレードと翼端渦の位置を1°刻みに補間し、方位角方向の精度向上を図った上で、渦によってブレード上に誘導される誘導速度を算出する。これをもとに、3段階目で3次元非定常オイラー方程式を解くCFDコードによる空力計算を行う。ここで得られたブレード上の圧力分布から、4段階目のFfowcs
Williams and Hawkings (FW-H)の式に基づく空力音響コードで、任意の観測点における音圧、即ち騒音を計算することになる。
2.2 移動重合格子法[2]
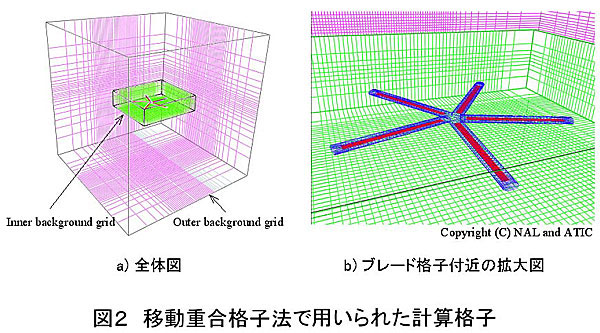
本解析法では、前述のトリム解析で得られた情報の内、ブレード運動のみをCFDコードに引き渡し、ブレードと渦との干渉を移動重合格子法によるCFDコードで直接捉える。本方法では計算格子として、ブレード格子、内側背景格子、外側背景格子の3種類を適用した(図2)。ブレード格子は、ブレード周りを覆いブレードと共に回転運動を行う物体適合座標の格子である。また、内側と外側の背景格子はともに空間に固定された直交座標の格子であり、前者はロータの回転する領域を覆う細かい格子、後者は計算領域全体を覆う粗い格子である。この方法では、それぞれの格子間で流れの情報を交換するために内挿を用いるが、この部分に費やす多大なCPU時間が問題となる。そこで、ベクトル・並列計算機であるNWTに向いた新たな内挿アルゴリズムを開発し、計算時間の短縮化を図った。結果として得られたブレード上の圧力分布から、前述した空力音響コードで任意の観測点における音圧を求める。
|
|
3.得られた成果
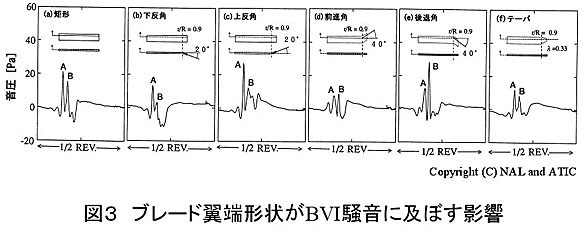
3.1 ブレードの翼端形状がBVI騒音に与える影響
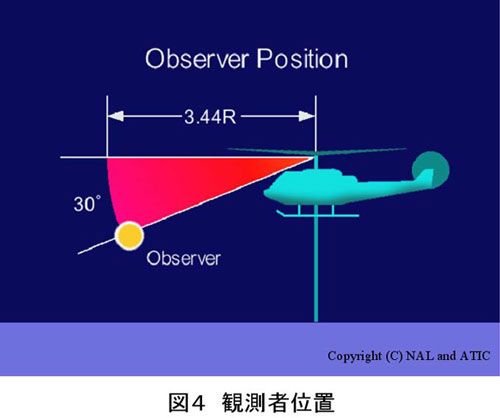
BVI騒音の強さは、1)ブレードと渦の垂直距離、2)ブレードと渦線との交差角度、3)渦の強さ及びコア半径、の3つに大きく影響されると言われている。ここでは、それぞれの要因に対応させて、翼端に上/下反角、前進/後退角、テーパを持つブレードを考え、これらの形状がBVI騒音の音圧波形に及ぼす影響を2.1節の方法を用いて解析した(図3)。計算対象は、2枚のブレードを持つ1/7スケールのモデル・ロータ[3]で、作動条件は、推力係数0.0054、ホバリング翼端マッハ数0.664、前進比0.164、シャフト傾角(後傾が正)2°である。また、観測者位置を図4に示す。
まず、下反角を付けた場合、ブレードと渦の垂直距離が大きくなるため、図3(b)のように矩形に比べて騒音は小さくなる。一方、上反角を付けた場合、垂直距離は小さくなるので、図3(c)のように騒音は大きくなってしまう。次に、前進角では前進側の翼端付近でブレードと渦線の交差角度が非常に大きくなり、垂直に近い干渉が起こるので、図3(d)のように騒音は小さくなる。逆に、後退角では交差角度が小さくなり、平行に近い干渉が起こるので、図3(e)のように騒音は大きくなる。最後に、翼端渦のコア半径として矩形のものよりも大きな値を用いたテーパのケースでは、ブレードが一周する間の荷重の時間変動が小さくなり、図3(f)のように騒音も小さくなる。
以上の計算結果を可聴化することによって、実際に人間の耳にどのように聞こえるか確認する研究も行った。この結果をビデオにした作品は、日本機械学会のビデオコンテストで最優秀賞と芸術賞を、また日経サイエンス社の主催するコンテストでも最優秀賞を受賞し、月刊誌『日経サイエンス』に掲載されるとともに、いくつかのテレビ局で科学番組の一部として放映された。
|
|
|
3.2 移動重合格子法によるBVI現象の直接解析
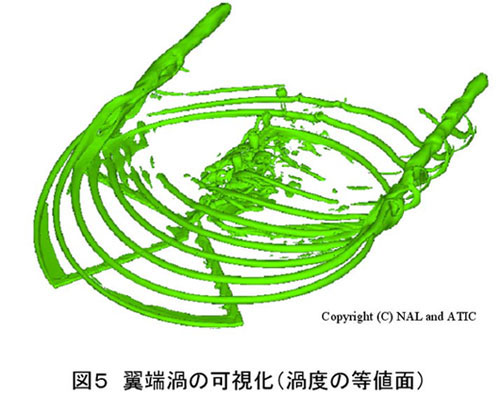
図5は、2.2節の方法で得られた流れ場の結果から渦度の等値面によって翼端渦を可視化したものである。計算対象は、ATICがドイツ・オランダ共用風洞(DNW)において行った実験で用いられたロータ半径(R)2mの5枚ブレード・モデル・ロータ[4]であり、作動条件は、推力係数0.0064、ホバリング翼端マッハ数0.63、前進比0.16、シャフト傾角(後傾が正)4.5°である。また、観測者位置はロータ中心から2R前方の30°斜め下方とした。この計算における格子点数は合計約1700万点であり、CPU時間は30PEでロータ一回転当たり約20時間であった。ただし、周期解を得るために約4回転の計算を必要とした。図5より、ブレードの先端から放出された翼端渦が後続ブレードと干渉する様子がよく捉えられているのがわかる。
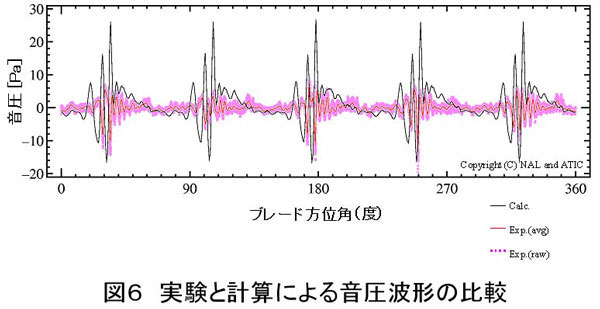
図6に、この結果を用いて空力音響コードによって計算された音圧波形と実験値との比較を示す。実験値は生データ(Exp.(raw))と平均化した値(Exp.(avg))をともに示した。計算結果は実験値を過大予測しているものの、CFDによるBVI現象の直接解析によって、世界で初めてBVI騒音の特徴であるインパルシブな音圧波形を捉えることに成功した。過大予測の原因としては、トリム解析の結果と実験値との不一致、ブレードの弾性変形や胴体の影響を考慮していないこと等が考えられる。
|
|
|
4. まとめと今後の課題
トリム計算、CFDによる空力計算及び波動方程式を解く空力音響計算を組み合わせた方法を用いて、ブレードの翼端形状がBVI騒音に及ぼす影響を把握することができた。また、CFDによってBVI現象を直接解析するコードを開発し、BVI騒音の特徴であるインパルシブな音圧波形を捉えることに世界で初めて成功した。
今後の課題としては、ブレードの弾性変形も考慮できる空力/構造連成問題解析コード及び、胴体も含めたヘリコプタ全機周りの流れ場解析コードの開発等が挙げられる。
参考文献
- Aoyama, T. et al., Calculation of
Rotor Blade-Vortex Interaction Noise using Parallel Super Computer, 22nd ERF,
No.8, 1996.
- Ochi, A. et al., BVI Noise Predictions
by Moving Overlapped Grid Method, AHS 55th Annual Forum, Montreal, Quebec,
Canada, May 25-27, 1999.
- Splettstoesser, W. R. et al., Helicopter Model Rotor Blade Vortex Interaction
Impulsive Noise: Scalability and Parametric Variations, 10th ERF, Nr.18, 1984.
- Murashige, A. et al., ATIC Aeroelastic Model Rotor Test at DNW, 24th ERF,
No.AC02, 1998.
|
|



