数値風洞と乱流の直接シミュレーション
航空宇宙技術研究所
山本稀義
1.計算機の発達と乱流の数値シミュレーション
乱流は自然界の流れの中では頻繁に発生する極めてありふれた流体現象であるにも関わらず、 流れの強い非線形作用によって著しく不規則に変動する速度場が発生することが特徴である。
そのような不規則な速度変動の力学法則を表現するためには統計理論に基づく記述が必要とな るため、乱流の理論的、実験的解明には現在でも多くの困難が残されている。しかし、近年の
計算機の飛躍的な進歩はそのような乱流研究についても数値シミュレーションという第3の研 究手法をもたらした。
乱流の数値シミュレーションには流れの平均量に関するモデル方程式を計算する方法と流れ の基礎方程式であるナビェ・ストークス方程式を計算する直接シミュレーションがある。前者
は速度場の平均値を取り扱うため計算量が比較的少なくてすむ利点があるので、計算機の性能 がそれほど発達していなかった1960年代から乱流の研究に応用されてきた。反面、基礎となる
モデル方程式の中に人工的な乱流モデルを含むので、得られた計算結果が使用された乱流モデ ルに依存する欠点があり、高精度な乱流モデルの考案がこの方法の課題として今日まで残され
ている。これに対して、直接シミュレーション(DNS)は乱流の速度場をナビェ・ストークス方 程式の初期値問題として直接計算するので、乱流の速度変動がそのまま得られる利点はあるが、
反面、取り扱う計算量が膨大になるため計算機の性能が発達した1980年頃から盛んになってきた 方法である。
当所に於いても1977年にわが国初のベクトル型計算機であるFACOM230-75APUが、さらに、 1987年にVP-400が導入されたことによって3次元乱流のDNSがようやく可能となってきた。
具体的には、等方性乱流のDNSが前者を使用しては空間格子点数が643まで実施され、後者に よっては1283まで実施された。しかし、これらのDNSで計算された乱流のレイノルズ数はまだ
小さいため、高レイノルズ数乱流の実験において観測される種々の普遍的な力学法則を実証す るには不十分であった。これに対して、1993年に導入された数値風洞(NWT)を使用した場合、
前記のDNSの空間格子点数は5123まで大きくすることが可能となり、その結果、乱流レイノル ズ数も約2倍に大きくすることが可能となった(参考文献1参照)。また、工学的にも重要なせん
断流である平板境界層やチャンネル流などの非等方的な乱流のDNSも実行出来るようになった。(参考文献2参照)
2.等方性乱流のDNS
等方性乱流は固体境界より遠く離れた流れの中に実現する理想的な乱流であるが、その速度場の 解析から乱流の基本的な力学法則を明らかにする目的で、理論的にも実験的にも広く研究されてい
る乱流である。DNSは流れの中に周期的境界条件を課した流体の立方体を考え、その中の速度場を乱流 の初期値問題としてナビェ・ストークス方程式から計算する。この時、ナビェ・ストークス方程式
の計算には空間的な計算精度の良いフーリェ・スペクトル法が応用された。
前記の様に、等方性乱流のDNSはVP-400によって空間格子点数が1283まで実行された。しかし、 格子点数1283の計算によっても得られた乱流のマイクロスケールに基づいたレイノルズ数Rλはま
だ90程度であったので、高レイノルズ数乱流に特有な普遍的な力学法則を定量的に検証することは 難しかった。これに対して、NWTはVP-400に比べて100倍以上の性能を有するので、空間格子点数と
してはVP-400の64倍である5123のDNSが可能となった。表1はVP-400とNWTによって実行された等 方性乱流のDNSにおける計算パラメータの比較を示す。この計算に使用されたNWTのPE台数は128台で、
並列化の特性もほぼ理想的な並列性能が実現された。空間格子点数の増加に伴って計算の時間ステッ プΔtも小さくする必要があったが、結局、NWTの128台のPEを使用することによって偶然的にもVP-400
の128倍の空間格子点数の流れの計算が同1の計算時間(CPU)で実現出来るようになった。その結果、 乱流のレイノルズ数Rλは160と2倍近くまで大きくすることが出来た(参考文献1参照)。また、本計
算の計算速度は応用計算としては最速である90ギガフロップスに到達した。
|

表1 VP-400とNWTで実行された等方性乱流の計算パラメータ
|
NWTによる空間格子点数5123のDNSによって検証された普遍的な乱流の力学法則として、エネルギ
ースペクトルに関するコルモゴロフのスペクトルがある。コルモゴロフのスペクトルは高レイノルズ 数乱流の普遍的な法則として実験的にも実証されていて、これをDNSで検証出来たことは本DNSの有効
性を証明した結果でもある(参考文献1参照)。
図1は本DNSで得られた乱流速度場の渦度を可視化した結果で、極めて微細な多数の渦が観測されて いる。この結果は、乱流速度場の不規則な変動はこの様な微細な多数の渦によって誘起されていること
を示している。乱流中の渦としてはこれまでもカルマン渦や乱流混合層等の大規模な渦の存在はよく知 られていたが、粘性による散逸が支配的であるような微小なスケールにおいても渦構造が存在すること
はそれまで予想されていなかったことで、DNSによって発見できた乱流の重要な普遍的構造である。(参考文献1参照)
|

図1 発達した等方性乱流中に観測される微細な渦構造の可視化
表示されたのは格子点5123中の8分の1の2563格子点領域
|
3.せん断流遷移のDNS
固体壁近傍の境界層が乱流へ遷移する力学機構を知ることは翼面境界層の遷移位置の予測や遷移の制 御技術の開発に関連して重要である。境界層の遷移機構としては線形安定理論によって予測されている
トルミーン・シュリフティンク波(TS波)の不安定による遷移機構がよく知られているが、近年このTS 波によらない遷移機構(バイパス遷移)も重要であることが認識されるようになってきた。一般的に言
えば、気流に含まれている撹乱や壁面の粗さが小さい場合にはTS波型遷移が発生するが、大きくなると バイパス遷移が実現することが知れられている。しかし、現実の流れの中でこれらの2種類の遷移機構の
どれが、何時、何処で発生するかを明確に予測できないことが遷移の予測を困難にしているのである。そ こで、流れの初期撹乱の大きさが遷移機構に及ぼす影響を調べる目的で、基本的なせん断流である平板境
界層および平面ポァズイユ流の遷移過程のDNSがNWTを使用して行われた。流れの計算には、壁面に垂直な 方向にはチェビシェフ級数展開、流れ方向およびスパン方向にはフーリェ級数展開を用いるチェビシェフ・
スペクトル法が使用された。NWTを使用することによってこれらの流れについて空間格子点数256×64×129 の計算をパラメトリックに実行することが可能となり、その結果、平面ポァズイユ流のDNSではレイノルズ
数が1000から40000まで計算可能となった。
図2は平面ポァズイユ流にバイパス遷移を誘起する初期撹乱の振幅u’の閾値を種々のレイノルズ数につ いて調べた結果を示す。振幅の閾値はレイノルズ数Rに依存し、ほぼR-1.7(実線)に比例する結果が導かれ
た。図2から、平面ポァズイユ流の遷移については初期撹乱の振幅に依存して以下の3つの状況が実現する ことがわかる。第1は初期撹乱の振幅が実線以上の場合で、この場合はバイパス遷移が実現する。第2は初期
撹乱の振幅が実線以下であるが、レイノルズ数がTS波型遷移の臨界レイノルズ数5772以上の場合で、この場 合はTS型遷移が実現する。第3は初期撹乱の振幅が実線以下で、かつ、レイノルズ数が5772以下の場合で、こ
の場合は乱流への遷移は実現しない(参考文献2参照)。
|
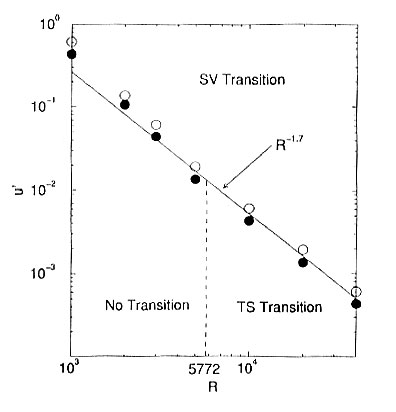
図2 平面ポァズイユ流のバイパス遷移を誘起する初期撹乱の振幅の閾値
○は遷移を誘起した振幅、●は遷移を誘起しなかった振幅を示す。
|
同様な乱流遷移に関する初期撹乱への依存性は平板境界層についても得られた。しかしながら、応用分野 で重要となる105以上の高レイノルズ数乱流のDNSを実現するためにはNWTをさらに越えた高速計算機が要望
されている。
参考文献
- 生出伸一、細川巌、山本稀義;パッシブスカラーを伴う減衰等方性乱流のDNS、ながれ、第6巻
(1997) 259-270.
- 山本稀義、高橋直也;平面ポァズイユ流のバイパス遷移、日本機械学会論文集(B編)68巻(2002)1030-1035.
|



