PROCESSORS指示文により、プロセッサ構成を宣言することができます。 プロセッサ構成 は、抽象プロセッサを配列形状に並べたもので 、HPFでは、各抽象プロセッサを処理単位として データマッピングと計算マッピングが行われます。
PROCESSORS指示文の構文は、付録の PROCESSORS指示文 の節を参照してください。
プロセッサ構成の形状は、プログラミングの都合により 自由に決めることができ、例えば、実際の並列コンピュータ のトポロジがメッシュだからといって、2次元配列にしなければならない、 といったことは全くありません。
プロセッサ構成の次元数は、配列を何次元分マップするか、 と言うことに対応しており、その結果、HPFプログラムが 何次元分並列化されるか、と言うことに対応しています。
例1: 1次元プロセッサ構成 → 1次元マッピング → 1次元並列化
REAL A(100,100)
!HPF$ PROCESSORS P(4)
!HPF$ DISTRIBUTE (*,BLOCK) ONTO P :: A
例2: 2次元プロセッサ構成 → 2次元マッピング → 2次元並列化
REAL A(100,100)
!HPF$ PROCESSORS P(2,2)
!HPF$ DISTRIBUTE (BLOCK,BLOCK) ONTO P :: A
例えば
HPF/ESの
場合、
通信は、MPIにより実装されており、
宣言されたプロセッサ構成の各要素、すなわち各抽象プロセッサは、
MPIプロセスと一対一に対応づけられます。
したがって、プロセッサ構成の大きさは、起動するMPIプロセス数
と同一でなければなりません。
このため、何次元の並列化であっても、並列度の総数は、起動した
MPIプロセス数と等しくなります。
通常は、1次元での並列化が、並列化のオーバヘッドを小さくしやすいため、
1次元プロセッサ構成を利用すればよいでしょう。
状況に応じて、起動する プロセス数を実行時に変えたい場合には、 組込み関数NUMBER_OF_PROCESSORS()を利用します。 この組込み関数は、起動された プロセス数を返します。
例3: NUMBER_OF_PROCESSORS()の利用
REAL A(100,100)
!HPF$ PROCESSORS P(NUMBER_OF_PROCESSORS())
!HPF$ DISTRIBUTE (*,BLOCK) ONTO P :: A
さらに、PROCESSORS指示文やDISTRIBUTE指示文中のONTO節を省略して、 以下のように記述しても、 HPFコンパイラは、 起動された プロセス数と等しい大きさのプロセッサ構成への マッピングが指定されたものとして扱いますので、 例3と全く同じように動作します。
例4: プロセッサ構成の省略
REAL A(100,100)
!HPF$ DISTRIBUTE (*,BLOCK) :: A
以下のように、 異なる形状のプロセッサ構成を混在させることも、 それらの大きさが等しければ許されますが、 異なる形状のプロセッサ構成上にマップされた 配列データが混在すると、 通信が必要 かどうかの判定が困難になる場合があるので、 特別な理由がない限り、避けた方が良いでしょう。
例5: 異なる形状のプロセッサ構成の混在
REAL A(100,100),B(100,100)
!HPF$ PROCESSORS P1(4),P2(2,2)
!HPF$ DISTRIBUTE (*,BLOCK) ONTO P1 :: A
!HPF$ DISTRIBUTE (BLOCK,BLOCK) ONTO P2 :: B
プロセッサ構成の各抽象プロセッサ上に、配列のどの部分が割り付けられるかは、 ALIGN指示文とDISTRIBUTE指示文により指定することができます。 DISTRIBUTE指示文は、プロセッサ構成上に配列をどのように割り付けるかを 指定する指示文です。ALIGN指示文は、 DISTRIBUTE指示文によってマッピングが指定された配列を基準として、 その配列との相対的な位置関係により、間接的にプロセッサ構成上への マッピングを指定する指示文です。
HPFコンパイラは、指定されたマッピング指示文、 配列の大きさ、および抽象プロセッサ数に基づいて、 抽象プロセッサ上に配列の各所有部分を割り付け、 各演算におけるデータのアクセス方法 とデータのマッピングを考慮して、 演算の各抽象プロセッサへの割り当てと必要な通信の生成を行います。
ここでは、まずDISTRIBUTE指示文を利用して、 色々なやり方でマッピングを指定する方法を見ていきます。 DISTRIBUTE指示文を利用して配列をマップすることを 分散 する、と言い、指定されたマッピングをその配列の分散と言います。
DISTRIBUTE指示文の構文は、付録の DISTRIBUTE指示文 の節を参照してください。
次のコードは、特に規則的な問題において、 最も汎用的な分散形式であるBLOCK分散によるHPFコード例です。
REAL X(16), Y(16)
!HPF$ DISTRIBUTE (BLOCK) :: X,Y
DO I=1,16
Y(I) = X(I)+1
ENDDO
この場合、代入文において、XとYの対応する要素は、
同じ抽象プロセッサ上に分散されているため、
HPFコンパイラは、利用可能な抽象プロセッサに、均等に演算を分割して、
通信なしで並列実行することができます。
例えば、このコードが4つの抽象プロセッサ上で実行される場合、
各抽象プロセッサ上に分散されている配列部分に基づいてループの
上下限が計算され、各抽象プロセッサは、それぞれループの以下のような範囲を
実行することになります。
! Processor 0
DO I = 1,4
Y(I) = X(I)+1
ENDDO
! Processor 1
DO I = 5,8
Y(I) = X(I)+1
ENDDO
! Processor 2
DO I = 9,12
Y(I) = X(I)+1
ENDDO
! Processor 3
DO I = 13,16
Y(I) = X(I)+1
ENDDO
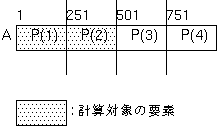
BLOCK分散は、基本的に、配列を均等に分割するための分散形式 であるため、例えば以下のように、必要なデータの大きさ (下の例ではN) が実行時に定まるような場合、 配列を大きめ (下の例では1000) に宣言しておいて、BLOCK分散でマップすると、 後の方の抽象プロセッサには、計算対象の要素が マップされず、不均等な作業負荷の原因となります。
DIMENSION A(1000)
!HPF$ PROCESSORS P(4)
!HPF$ DISTRIBUTE A(BLOCK) ONTO P
...
READ(*,*)N
DO I=1,N
A(I) = ...
例えば、上記のNの値が500だった場合、 計算対象の要素は、以下のようにP(1)とP(2)のみに マップされ、P(3)とP(4)が遊んでしまうことになります。

|
必要な大きさが実行時に定まる場合には、以下のように、 割付け配列や自動割付け配列により、動的に必要な大きさを 割り付けるのが良いでしょう。
DIMENSION, ALLOCATABLE :: A(:) ! 割付け配列
!HPF$ PROCESSORS P(4)
!HPF$ DISTRIBUTE A(BLOCK) ONTO P
...
READ(*,*)N
ALLOCATE (A(N))
DO I=1,N
A(I) = ...
...
CALL SUB(N)
...
SUBROUTINE SUB(N)
DIMENSION B(N) ! 自動割付け配列
!HPF$ PROCESSORS P(4)
!HPF$ DISTRIBUTE B(BLOCK) ONTO P
割付け配列に関する注意事項に関しては、 割付け配列 の節も参照してください。
BLOCK分散の分散ブロックサイズを、以下のように明示的に 指定することもできますが、
REAL X(16)
!HPF$ PROCESSORS P(2)
!HPF$ DISTRIBUTE (BLOCK(8)) ONTO P :: X
どの抽象プロセッサにもマップされない要素が存在しては ならないため、以下のような指定は許されません。
REAL X(16)
!HPF$ PROCESSORS P(2)
!HPF$ DISTRIBUTE (BLOCK(7)) ONTO P :: X
実際、上記の場合、X(15)とX(16)はどの抽象プロセッサにも マップされなくなってしまいます。
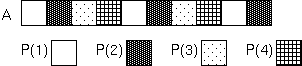
CYCLIC分散により、配列の各要素を、 ラウンドロビン方式で抽象プロセッサ上に分散することができます。
DIMENSION A(10)
!HPF$ PROCESSORS P(4)
!HPF$ DISTRIBUTE A(CYCLIC) ONTO P
|
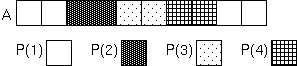
CYCLIC分散の分散ブロックサイズは、 以下のように明示的に指定することもできます。
DIMENSION A(10)
!HPF$ PROCESSORS P(4)
!HPF$ DISTRIBUTE A(CYCLIC(2)) ONTO P
|
CYCLIC分散は、 負荷分散 のために利用することができます。
次の例は2つの三角行列、BとCを加算し、結果をAに格納するものです。
INTEGER, PARAMETER :: N=1000
INTEGER A(N,N),B(N,N),C(N,N)
DO I=1,N
DO J=1,I
A(I,J)=B(I,J)+C(I,J)
ENDDO
ENDDO
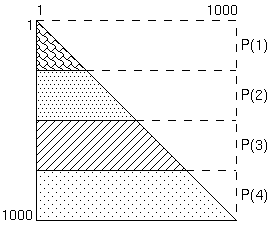
例えば、各三角配列の1次元目を4つの抽象プロセッサにBLOCK分散する場合、
4つの抽象プロセッサのそれぞれに対して、各配列の
250の行がマップされることになります。
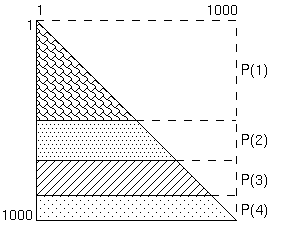
三角行列のI行目にはI個の非零要素があるため、この場合、各配列に関して、
P(1)上の行1-250については、31375個の計算対象の要素が、
P(2)上の行251-500については、93875個の計算対象の要素が、
P(3)上の行501-750については、156375個の計算対象の要素が、
P(4)上の行751-1000については、218875個の計算対象の要素が、
それぞれマップされることになります。
|
つまり、この例では、単純なBLOCK分散は不均等な作業負荷の原因となります。
このような場合、以下のように、 CYCLIC分散を利用すれば、作業負荷の均等化をはかることができます。
INTEGER, PARAMETER :: N=1000
INTEGER A(N,N),B(N,N),C(N,N)
!HPF$ PROCESSORS P(4)
!HPF$ DISTRIBUTE (CYCLIC,*) ONTO P :: A,B,C
DO I=1,N
DO J=1,I
A(I,J)=B(I,J)+C(I,J)
ENDDO
ENDDO
この場合、
P(1)上の行1,5,9,...,997については、124750個の計算対象の要素が、
P(2)上の行2,6,10,..,998については、125000個の計算対象の要素が、
P(3)上の行3,7,11,..,999については、125250個の計算対象の要素が、
P(4)上の行4,8,12,..,1000については、125500個の計算対象の要素が、
それぞれマップされることになります。
BLOCK分散で分散された配列の次元は、連続した要素が、 各抽象プロセッサ上に割り付けられるため、 BLOCK分散時の中間ソースにおける添字 の図のように、 HPFコンパイラ が生成するSPMDモデルの中間ソースにおいて、 配列の宣言範囲を、 各抽象プロセッサ上に マップされている範囲に変えるだけで、 HPFソースプログラム上での配列の添字 (これを、 グローバル添字 と言います) と、 HPFコンパイラ が生成するSPMDモデルの中間ソース上での添字 (これを、 ローカル添字 と言います) を同一にすることができます。
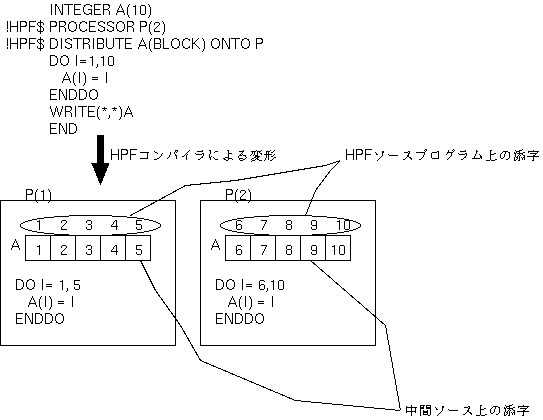
|
それに対して、CYCLIC分散で分散された配列の次元は、不連続な要素が、 各抽象プロセッサ上に割り付けられる際に、メモリ上連続になるよう配置されるため、 CYCLIC分散時の中間ソースにおける添字 の図のように HPFソースプログラム上での配列の添字と、 HPFコンパイラ が生成するSPMDモデルの中間ソース上での添字とが異なります。
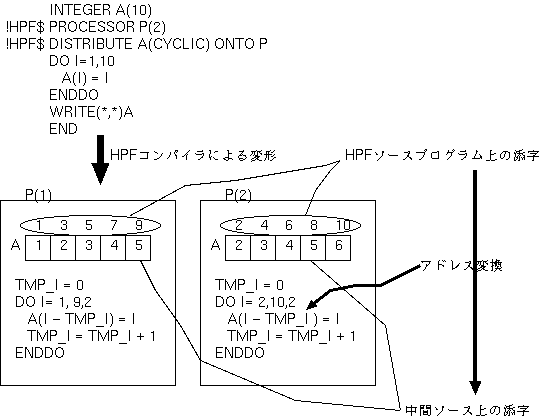
|
このようなグローバル添字からローカル添字への変換を アドレス変換 といい、CYCLIC分散では、BLOCK分散に比べてアドレス変換の オーバヘッドが伴うことに注意する必要があります。
一般化されたBLOCK分散であるGEN_BLOCK分散によって、 配列の均等でない大きさの連続的な切片を、 抽象プロセッサ上にマップすることができます。
GEN_BLOCK分散もまた、不均等な計算を行うアルゴリズムに対して、 その作業負荷のバランスをとるために用いることができます。 一般的には、CYCLIC分散よりも、GEN_BLOCK分散の方が、 並列化の粒度を大きくし易く、アドレス変換の必要がなく、 さらに後述する シフト転送 のようなオーバヘッドの少ない定型的な通信が可能にな る可能性が高いため、負荷分散の手段としては優れていると言えます。
次の例は、先の例と同様の演算において、GEN_BLOCK分散で
分散することにより、負荷分散を図った
コードです。
Nを三角行列の行数とするとき、三角行列の非零要素の数がN*(N+1)/2に等しいことに
留意すれば、以下のような方法により、
GEN_BLOCK分散で各抽象プロセッサへマップされる要素数を
指定するための
マッピング配列
(下の例では配列GB) の値を計算することができ、
作業負荷のバランスをとることが可能になります。
INTEGER,ALLOCATABLE :: GB(:)
INTEGER,PARAMETER :: N=1000
! 計算対象の全要素数の計算
IWORK = (N*(N+1)/2)
! マッピング配列の割り付け
ALLOCATE(GB(NUMBER_OF_PROCESSORS()))
! マッピング配列を初期値を0で初期化する。
GB = 0
! 抽象プロセッサ一台当りの計算対象の要素数を計算する
IEACH = IWORK / NUMBER_OF_PROCESSORS()
! マッピング配列の添字を1に初期化
IGB = 1
! 計算対象の要素数を0に初期化
ITHIS = 0
! 各行に関する計算
DO I = 1,N
! 第I行目の計算対象の要素数を加える
ITHIS = ITHIS + I
! IGB番目の抽象プロセッサにマップされる行の数を1増やす。
GB(IGB) = GB(IGB) + 1
! 計算対象の要素数が抽象プロセッサ一台分以上になれば、次のGBの要素を計算
IF ( ITHIS .GE. IEACH ) THEN
IGB = IGB + 1
ITHIS = 0
ENDIF
ENDDO
CALL SUM_TRIANGULAR(GB)
DEALLOCATE(GB)
END
SUBROUTINE SUM_TRIANGULAR(GB)
INTEGER,DIMENSION(NUMBER_OF_PROCESSORS()) :: GB
INTEGER,PARAMETER :: N=1000
INTEGER A(N,N),B(N,N),C(N,N)
!HPF$ PROCESSORS P(NUMBER_OF_PROCESSORS())
!HPF$ DISTRIBUTE (GEN_BLOCK(GB),*) ONTO P :: A,B,C
DO I=1,N
DO J=1,I
A(I,J)=B(I,J)+C(I,J)
ENDDO
ENDDO
この場合、抽象プロセッサ数が4だとすると、各配列に関して、
P(1)上の行1-500については、125000個の計算対象の要素が、
P(2)上の行501-708については、125382個の計算対象の要素が、
P(3)上の行709-867については、124859個の計算対象の要素が、
P(4)上の行868-1000については、123722個の計算対象の要素が、
それぞれマップされることになります。
|
計算内容に応じて、適切な分散形式は異なります。
多くの場合、
各配列要素に対する処理量が概ね均等であるならばBLOCK分散、
不均等であるならばGEN_BLOCK分散を選択するのが良いでしょう。
これら2つの分散形式は、
ために、CYCLIC分散やINDIRECT分散よりも高い実行性能を得やすい からです。
INDIRECT分散に関しては、 不規則問題のための指示文 の節で 解説します。
ALIGN指示文は、DISTRIBUTE指示文によって分散が指定された配列を基準として、
その配列との相対的な位置関係により、間接的に
プロセッサ構成上への
マッピングを指定する指示文です。
ALIGN指示文により、ある配列と、基準となる配列との間の
対応関係を
指定することを、
整列
する、と言い、基準となる配列を
整列先
、整列を指定された配列を
alignee
といいます。
ALIGN指示文の構文は、付録の ALIGN指示文 の節を参照してください。
ALIGN指示文によって、多様なマッピングが可能となりますが、 特に、DISTRIBUTE指示文だけでは、リモートアクセスが 発生しないマッピングの指定が不可能である場合に利用すると有効です。
以下のコードは、通信が必要となるマッピング指定の例です。
REAL X(15), Y(16)
!HPF$ PROCESSORS P(2)
!HPF$ DISTRIBUTE (BLOCK) ONTO P :: X,Y
DO I=1,15
X(I)=Y(I+1)
ENDDO
この場合、
P(1)にマップされる X(8)に、代入文 X(I)=Y(I+1) において対応する要素Y(9)は、
P(2)にマップされます。そのため、I=8の繰り返しの実行に備えて、
HPFコンパイラは、通信を生成することになります。
この通信は、以下のように、ALIGN指示文を利用して
X(I)とY(I+1)を対応づけ、同じ抽象プロセッサ上にマップすることで、
抑制することが可能です。
REAL X(15), Y(16)
!HPF$ PROCESSORS P(2)
!HPF$ DISTRIBUTE Y(BLOCK) ONTO P
!HPF$ ALIGN X(I) WITH Y(I+1)
DO I=1,15
X(I)=Y(I+1)
ENDDO
次のコードは、配列の宣言サイズが異なるために、 BLOCK分散では、リモートアクセスが発生してしまう例です。
REAL X(15), Y(17)
!HPF$ PROCESSORS P(NUMBER_OF_PROCESSORS())
!HPF$ DISTRIBUTE (BLOCK) ONTO P :: X,Y
DO I=1,15
X(I)=Y(I)
ENDDO
例えば、NUMBER_OF_PROCESSORS()の値が2の場合、
Xの分散ブロックサイズは、(15-1)/2 + 1 = 8
Yの分散ブロックサイズは、(17-1)/2 + 1 = 9
となります。
そのため、P(2)にマップされる X(9)に、代入文 X(I)=Y(I) において
対応する要素Y(9)は、
P(1)にマップされます。そのため、I=9の繰り返しの実行に備えて、
HPFコンパイラは、通信を生成することになります。
この通信は、以下のように、ALIGN指示文を利用して
X(I)とY(I)を対応づけ、同じ抽象プロセッサ上にマップすることで、
抑制することが可能です。
REAL X(15), Y(17)
!HPF$ PROCESSORS P(NUMBER_OF_PROCESSORS())
!HPF$ DISTRIBUTE (BLOCK) ONTO P :: Y
!HPF$ ALIGN X(I) WITH Y(I)
DO I=1,15
X(I)=Y(I)
ENDDO
DISTRIBUTE指示文ではなく、ALIGN指示文を利用すべき 重要な例として、配列の上下限値が変数の場合があります。
N = 16
M = 16
CALL SUB(N,M)
END
SUBROUTINE SUB(N,M)
INTEGER X(N),Y(M)
!HPF$ PROCESSORS P(2)
!HPF$ DISTRIBUTE (BLOCK) ONTO P :: X,Y
CALL INIT(Y)
DO I=1,N
X(I)=Y(I)
ENDDO
WRITE(*,*)X
END
上記の例では、配列X、Yの上限値が翻訳時には不明な変数であるため、 BLOCK分散による分散ブロックサイズも翻訳時には不明な値となります。 そのため、 HPFコンパイラは、 DO Iのループをリモートアクセス なしで並列実行可能かどうかを判断することができず、 その結果、 例えばHPF/ESの場合、 リモートアクセスが必要な場合に備えて、以下のような 中間ソースを生成します。
LB = ( (N-1)/2+1 ) * MYID
ALLOCATE (TMP_Y(LB+1 : LB+(N-1)/2+1)) ! 一時領域の割り付け
call comm( TMP_Y <- Y ) ! Yの値を一時領域にコピー
DO I= LB+1, LB+(N-1)/2+1
X(I)=TMP_Y(I)
ENDDO
DEALLOCATE (TMP_Y)
上記中間ソースでは、DO Iのループは、各抽象プロセッサが
Xの所有範囲を実行するように並列化されますが、
Yに対するリモートアクセスの可能性に備えて、
一時領域TMP_Yが割り付けられ、Yの値をTMP_Yにコピーするための通信コードが
挿入されています。
この場合、実際には、リモートアクセスは必要でないため、
実行時に通信コードで行われるのは、各抽象プロセッサ内で、
Yの値をTMP_Yにコピーする処理だけですが、割り付けとコピーのための
オーバヘッドと、一時領域のための余分なメモリ領域が必要となってしまいます。
この例から、HPFプログラムにおいて、リモートアクセスの有無が翻訳時に
判定可能であることの重要性が分かります。
翻訳時に、リモートアクセスが発生する可能性のある場合、
たとえ、実行時にリモートアクセスが不要であることが分かったとしても、
翻訳時に分かっている場合に比べて、一時領域の割り付け/解放とコピー、
通信の必要性の判定のためのオーバヘッド、および一時領域のためのメモリ領域が
必要になってしまうからです。
したがって、可能な限り、翻訳時に配列のマッピングが
確定するようにプログラミングをすることは、
HPFプログラミングにおける一つの重要なポイントとなります。
上記の例においても、以下のように、
ALIGN指示文によって、X(I)とY(I)を対応づけることにより、
HPFコンパイラは、
翻訳時にリモートアクセスが不要であることを確定することができ、
SUBROUTINE SUB(N,M)
INTEGER X(N),Y(M)
!HPF$ PROCESSORS P(2)
!HPF$ DISTRIBUTE (BLOCK) ONTO P :: X
!HPF$ ALIGN (I) WITH X(I) :: Y
CALL INIT(Y)
DO I=1,N
X(I)=Y(I)
ENDDO
WRITE(*,*)X
END
その結果、以下のように、一時領域の割り付けや通信コードのない 効率の良い中間ソースを生成することができます。
LB = ( (N-1)/2+1 ) * MYID
DO I= LB+1, LB+(N-1)/2+1
X(I)=Y(I)
ENDDO
特に 形状引継配列 や、割付け配列の場合には、上下限値が、実行時に定まるので、 DISTRIBUTE指示文だけでなく、ALIGN指示文を積極的に利用して、 配列相互の位置関係を指定すると、HPFコンパイラの リモートアクセス解析を助け、性能向上に大いに役立ちます。
例)形状引継配列
SUBROUTINE SUB(X,Y)
INTEGER :: X(:),Y(:)
!HPF$ PROCESSORS P(2)
!HPF$ DISTRIBUTE (BLOCK) ONTO P :: X
!HPF$ ALIGN (I) WITH X(I) :: Y
例)割付け配列
INTEGER,ALLOCATABLE :: X(:),Y(:)
!HPF$ PROCESSORS P(2)
!HPF$ DISTRIBUTE (BLOCK) ONTO P :: X
!HPF$ ALIGN (I) WITH X(I) :: Y
以下の例では、行列ベクトル積の計算を DO Iのループで並列化するために、配列Aを1次元目で BLOCK分散し、YをAの対応する要素に整列させています。
INTEGER A(N,N),X(N),Y(N)
!HPF$ DISTRIBUTE A(BLOCK,*)
!HPF$ ALIGN Y(I) WITH A(I,*)
DO I=1,N
DO J = 1, N
Y(I) = Y(I) + A(I,J) * X(J)
ENDDO
ENDDO
この場合、Yの各要素は、Aの2次元目に対応するDO Jの
ループ中では、全ての繰り返しでアクセスされますから、
ALIGN指示文の整列先であるAの2次元目には、'*'が
指定されています。
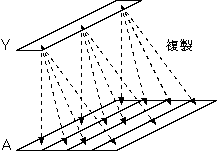
この整列は、
複製
の図のように、
Aの2次元目の任意の要素が
マップされる抽象プロセッサ上に、Yもまたマップされることを意味しており、
複製
と呼ばれます。
|
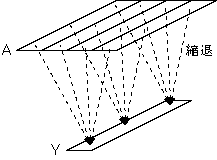
一方、以下の例では、Yを基準として、配列AをYに整列させています。
この場合、
ALIGN指示文のaligneeであるAの2次元目の添字は、
YとAとの対応関係に無関係なので、'*'が指定されています。
この整列は、
縮退
の図のように、
Aの2次元目の添字とは無関係に、
Aの1次元目とYの1次元目の対応する要素を、同じ抽象プロセッサ上に
マップすることを意味しており、
縮退
と呼ばれます。
INTEGER A(N,N),X(N),Y(N)
!HPF$ DISTRIBUTE Y(BLOCK)
!HPF$ ALIGN A(I,*) WITH Y(I)
DO I=1,N
DO J = 1, N
Y(I) = Y(I) + A(I,J) * X(J)
ENDDO
ENDDO
|
複製と縮退は、次元数の異なる配列同士を整列する際に有効です。
TEMPLATE指示文は、ALIGN指示文において、基準となる
適当な配列が存在しない場合、ALIGN指示文の指定のためだけに、
わざわざ不要な配列を宣言しなくて良いように、
メモリ領域を持たない仮想的な配列を宣言することができる
指示文です。
TEMPLATE指示文で宣言した配列を
テンプレート
と言います。
DISTRIBUTE指示文により分散が指定されたテンプレートを、
ALIGN指示文の整列先に指定する基準配列として利用することができます。
TEMPLATE指示文の構文は、付録の TEMPLATE指示文 の節を参照してください。
次の例は、プログラマが避けるべき
誤ったマッピングを示しています。
実際、ALIGN指示文中の
変数I (これを
align-dummy
といいます。) は、
aligneeであるXの宣言範囲の全ての添字値に
対して有効でなければなりません。
ところが、Iの値が、Xの宣言範囲である1から16まで変化するとき、
Y(16+1)という整列先Yの宣言範囲を越えた不正な参照が行われます。
これは翻訳時、あるいは実行時エラーの原因となります。
REAL X(16), Y(16)
!HPF$ DISTRIBUTE Y(BLOCK)
!HPF$ ALIGN X(I) WITH Y(I+1)
DO I=1,15
X(I)=Y(I+1)
ENDDO
このような場合には、以下のように、TEMPLATE指示文を利用して、 ALIGN指示文の指定に必要な範囲の上下限を持つ テンプレートを宣言することにより、記憶領域を浪費することなく、 適切なマッピングを表現することができます。
REAL X(16), Y(16)
!HPF$ TEMPLATE T(17)
!HPF$ DISTRIBUTE T(BLOCK)
!HPF$ ALIGN X(I) WITH T(I+1)
!HPF$ ALIGN Y(I) WITH T(I)
DO I=1,15
X(I)=Y(I+1)
ENDDO
TEMPLATE指示文は、以下のように、複数の配列の宣言範囲が 異なる場合にも有効です。
REAL A(16),B(0:16),C(1:17)
DO I=1,16
A(I) = B(I) + C(I)
ENDDO
上記の例では、宣言範囲が異なるので、リモートアクセスが生じないように、
BをAやCに整列することも、CをAやBに整列することもうまくできません。
このような場合には、以下のように、B、Cの宣言範囲を
包含するようなテンプレートを宣言して、基準配列として
利用することで最適なマッピングが表現できます。
REAL A(16),B(0:16),C(1:17)
!HPF$ TEMPLATE T(0:17)
!HPF$ DISTRIBUTE T(BLOCK)
!HPF$ ALIGN (I) WITH T(I) :: A,B,C
DO I=1,16
A(I) = B(I) + C(I)
ENDDO
HPFプログラムから他のHPF手続を引用する場合、
実引数と
対応する仮引数との間で、マッピングが同じである必要は必ずしも
ありません。
以下の例では、主プログラム
において、
実引数Aは、1次元目でBLOCK分散されているのに対して、
呼出先手続SUBの対応する仮引数Aは、2次元目でBLOCK分散されています。
PROGRAM MAIN
INTEGER A(10,10)
!HPF$ DISTRIBUTE (BLOCK,*) :: A
CALL SUB(A)
:
SUBROUTINE SUB(A)
INTEGER A(10,10)
!HPF$ DISTRIBUTE (*,BLOCK) :: A
実引数と対応する仮引数のマッピングが異なる場合には、
呼出先手続の起動時に、仮引数のマッピングに合わせるための
通信が、また呼出元手続への戻り時に、実引数のマッピングに
戻すための通信が、それぞれ暗黙的に発生することに注意する必要があります。
逆に、手続内でのマッピングの変更を避けるために、
意図的に手続境界でマッピングの変更を行うことが
有効な場合もあります。 (
動的再マッピング
の節を参照してください。)
上記のことから、呼出元手続における 実引数のマッピングは、 たとえ、対応する仮引数のマッピングが異なる場合にも、 決して変更されないことが分かります。 この例の場合、主プログラムにおける配列Aのマッピングは、 サブルーチンSUBから戻った後も、1次元目のBLOCK分散のままとなります。
上記の例のように、実引数と対応する仮引数のマッピングが
異なる場合、
一般的には、
明示的引用仕様がなくても手続境界での再マッピングが可能です。
(これは、HPF2.0仕様上は禁じられています。)
ここで、
明示的引用仕様
とは、Fortran規格の用語で、
引用する手続に対する
引用仕様宣言 (interface block)
を記述したり、モジュール副プログラムや内部副プログラムとして
記述したりすることにより、
引用する手続の総称名や、仮引数の属性などを、
呼出元に明示することを言います。
ただし、明示的引用仕様
には、
INTENT属性など、コンパイラによる最適化に役立つ情報が含まれていますので、
積極的に記述することを推奨します。
また、仮引数が形状引継配列であることなどにより、
Fortran規格上明示的引用仕様が必要な場合や、
PURE手続/外来手続を引用する場合には、
明示的引用仕様を記述する必要があります。
以下のような隣接アクセスを含むコードを考えてみます。
PROGRAM TEST_SHIFT
INTEGER I,A(8),B(8)
!HPF$ PROCESSORS P(2)
!HPF$ DISTRIBUTE (BLOCK) ONTO P :: A,B
:
DO I=2,7
A(I)= B(I-1) + B(I) + B(I+1)
ENDDO
例えば
HPF/ESの場合、
各抽象プロセッサが
Aの所有範囲を実行するように、
このループを並列化します。
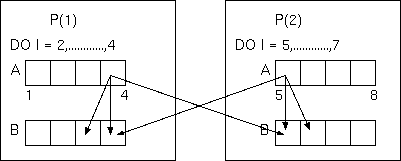
その結果、
隣接アクセスパタン
の図のように、
P(1)が、I=4の繰り返しを実行する際に、
P(2)上にマップされているB(5)の値が、
また、P(2)がI=5の繰り返しを実行する際に、
P(1)上にマップされているB(4)の値が必要となります。
|
この例では、どのようなマッピングを指定しても、
全く通信なしで並列化することはできません。
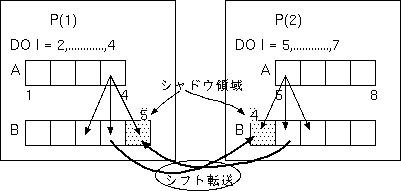
しかし、最初に
Bを各抽象プロセッサ上に割り付けるときに、
シフト転送
の図のように、
リモートアクセスに必要なサイズの
バッファ領域を上下方向にあらかじめ確保しておけば、
ループの並列実行前に、
隣接するプロセッサ間で通信を行って、
必要な値をバッファ領域に設定しておくことができ、
Bに対する一時領域を割り付けて、Bの値をその一時領域に通信/コピーするよりも、
はるかに小さなオーバヘッドで、並列実行を
行うことが可能になります。
|
このようなバッファ領域を
シャドウ領域
と呼び、
隣接プロセッサ間のシャドウ領域に対する通信を
シフト転送
といいます。
シフト転送は、各抽象プロセッサの通信量や通信相手が少なく、また
全プロセッサが同時に通信を行うことができるため、
最もオーバヘッドの少ない通信パタンであり、
通信なし、あるいはシフト転送のみで並列化可能なループだけからなる
HPFプログラムは、高いSpeed Upを期待することができます。
シャドウ領域の大きさは、プログラマが、SHADOW指示文により
明示的に指定することもできます。
SHADOW指示文が指定された場合、シャドウ領域の幅はその指示文により
決定されます。
配列下限側、あるいは上限側のシャドウ領域の幅は個々に指定可能であり、それらが同じ幅である必要はありません。
SHADOW指示文の構文は、付録の SHADOW指示文 の節を参照してください。
以下の例では、配列の1次元目に対してはシャドウ領域を割り付けないことを、 また2次元目の 下限側に1要素分のシャドウ領域を、 上限側に2要素分のシャドウ領域を割り付けることを指定しています。
!HPF$ DISTRIBUTE (*,BLOCK) :: A,B,C !HPF$ SHADOW (0,1:2) :: A,B,C
もし上下両端のシャドウ領域の幅が同じ2ならば、次の構文が使用できます。
!HPF$ DISTRIBUTE (*,BLOCK) :: A,B,C !HPF$ SHADOW (0,2) :: A,B,C
実引数と対応する仮引数の
シャドウ領域の幅が異なると、たとえ分散や整列が同じであっても、
実引数と仮引数との間で、シャドウ領域の幅を変更するために、領域の割り付けと
値のコピーが必要となります。
そのため、明示的にSHADOW指示文を指定する場合、
実引数と対応する仮引数には同じ幅のシャドウ領域を指定することが大切です。
SHADOW指示文には、プログラム全体を通じて必要となるシャドウ幅の最大値を
指定するのが良いでしょう。
プログラムの実行途中で、最適なマッピングが変化する場合、 宣言時に、DYNAMIC指示文を指定した配列に対しては、 REDISTRIBUTE指示文で分散を変更したり、REALIGN指示文 で整列を変更したりすることができます。
DYNAMIC指示文の構文は、付録の DYNAMIC指示文 の節を参照してください。
REDISTRIBUTE指示文の構文は、付録の REDISTRIBUTE指示文 の節を参照してください。
REALIGN指示文の構文は、付録の REALIGN指示文 の節を参照してください。
REAL A(N,N)
!HPF$ DISTRIBUTE A(*,BLOCK)
!HPF$ DYNAMIC A ! DYNAMIC指示文
DO J=1,N
DO I=2,N-1
A(I,J) = A(I+1,J) + A(I,J) + A(I-1,J)
ENDDO
ENDDO
!HPF$ REDISTRIBUTE A(BLOCK,*) ! REDISTRIBUTE指示文
DO I=1,N
DO J=2,N-1
A(I,J) = A(I,J+1) + A(I,J) + A(I,J-1)
ENDDO
ENDDO
上記の例では、最初のDOループネストでは、Iのループに繰り返し間の依存があり、
配列Aの2次元目に対応するJのループが並列化可能なので、
マッピングの指定も2次元目を分散するのが適切であるのに対して、
2番目のDOループネストでは、Jのループに繰り返し間の依存があり
配列Aの1次元目に対応するIのループが並列化可能なので、
マッピングの指定も1次元目を分散するのが適切です。
そのため、2つのループ間で、REDISTRIBUTE指示文により、
配列Aの分散を変更しています。
ただし、再マッピング処理には、通信のオーバヘッドが伴うため、 再マッピング後の演算量を出来るだけ大きくして、 通信オーバヘッドの影響を相対的に下げることが大切です。
さらに、DYNAMIC指示文が指定された配列は、
どのようなマッピングを持つかが、一般に翻訳時には判定できないため、
HPFコンパイラによる、最適な並列化とリモートアクセス解析を妨げます。
これを防ぐ最も簡単な方法は、
最適なマッピングが同一であるような処理毎に、別の手続に分割し、
各手続内ではDYNAMIC指示文を使用せずに、宣言時にその手続全体における
マッピングを指定する方法です。
上記の例の2つのループネストを、別の手続に分割すると、以下のようになります。
REAL A(N,N)
!HPF$ DISTRIBUTE A(*,BLOCK)
DO J=1,N
DO I=2,N-1
A(I,J) = A(I+1,J) + A(I,J) + A(I-1,J)
ENDDO
ENDDO
CALL SUB(A,N)
:
SUBROUTINE SUB(A,N)
REAL A(N,N)
!HPF$ DISTRIBUTE A(BLOCK,*)
DO I=1,N
DO J=2,N-1
A(I,J) = A(I,J+1) + A(I,J) + A(I,J-1)
ENDDO
ENDDO
順序結合 とは、以下の実引数A(1,1,I)と仮引数A(100,100) あるいは、実引数B(10000)と仮引数B(100,100)のように、 形状の異なる実引数と仮引数を結合することを言います。
INTEGER A(100,100,100),B(10000)
DO I=1,100
CALL SUB(A(1,1,I),B)
ENDDO
:
SUBROUTINE SUB(A,B)
INTEGER A(100,100),B(100,100)
記憶列結合 とは、以下の例の2つの配列AとB、 3つの配列C、D、E、あるいは 共通ブロックCOM2中の2つの配列F、Gのように、 EQUIVALENCE文、共通ブロック、 またはEQUIVALENCE文と共通ブロックの組合わせにより、 複数の実体の記憶領域を共有させることを言います。
SUBROUTINE SUB()
INTEGER A(10000),B(100,100)
EQUIVALENCE (A,B)
COMMON /COM1/C(100),D(100)
REAL E(200)
EQUIVALENCE (C,E)
COMMON /COM2/F(10000)
....
SUBROUTINE SUB2()
COMMON /COM2/G(100,100)
HPFでは、上記のように、形状の異なる配列同士が順序結合や
記憶列結合によって結合されている場合、それらをマップする
ことはできず、さらに、EQUIVALENCE文によるもの
以外の場合にはSEQUENCE指示文を指定して、順序結合や記憶列結合の利用を
明示する必要があります。
HPFのマッピングは、各次元毎に独立して指定されるため、
異なる形状の配列が同じメモリ領域を共有すると、
HPFコンパイラによるマッピングの管理が困難になるからです。
SEQUENCE指示文の構文は、付録の SEQUENCE指示文 の節を参照してください。
例えば、以下のコードを、そのままHPFコンパイラで翻訳、実行を行う ことはできません。
INTEGER A(100,100,100),B(10000)
DO I=1,100
CALL SUB(A(1,1,I),B)
ENDDO
:
SUBROUTINE SUB(A,B)
INTEGER A(100,100),B(100,100)
このような場合、以下のように、実引数と仮引数のそれぞれに、 SEQUENCE指示文を指定する必要があります。 もちろん、これらにマッピングを指定することは許されません。
INTEGER A(100,100,100),B(10000)
!HPF$ SEQUENCE A,B
DO I=1,100
CALL SUB(A(1,1,I),B)
ENDDO
:
SUBROUTINE SUB(A,B)
INTEGER A(100,100),B(100,100)
!HPF$ SEQUENCE A,B
マッピングを指定したい場合には、以下のように、 Fortranの部分配列引数を利用したり、宣言の形状を 書き換えたりして、 実引数と対応する仮引数の形状を同一にしなければなりません。
INTEGER A(100,100,100),B(100,100)
!HPF$ DISTRIBUTE A(*,*,BLOCK)
!HPF$ DISTRIBUTE B(*,BLOCK)
DO I=1,100
CALL SUB(A(:,:,I),B)
ENDDO
:
SUBROUTINE SUB(A,B)
INTEGER A(100,100),B(100,100)
!HPF$ DISTRIBUTE B(*,BLOCK)
また、共通ブロックに含まれる実体の 形状が、手続毎に異なる場合には、 以下のように、共通ブロック名に対して、SEQUENCE指示文を指定する必要があります。 この場合も、共通ブロック中の変数をマップすることは 出来なくなります。
SUBROUTINE SUB()
COMMON /COM2/F(10000)
!HPF$ SEQUENCE /COM2/
....
SUBROUTINE SUB2()
COMMON /COM2/G(100,100)
!HPF$ SEQUENCE /COM2/
主要な配列をマップできない場合、主要な演算部分における
並列化も行われなくなってしまうので、
HPFにおいて、効率的な並列プログラムを開発するためには、
主要な配列は、はじめから利用する次元数で宣言
する必要があります。
必要な大きさが実行時に確定する場合には、
割付け配列 (以下の配列A) や自動割付け配列 (以下の配列B) を利用して、
必要な大きさを動的に確保すると良いでしょう。
REAL,ALLOCATABLE :: A(:,:) ! 割付け配列
!HPF$ DISTRIBUTE A(*,BLOCK)
READ(6,*)N
ALLOCATE (A(N,N))
...
CALL SUB(N)
SUBROUTINE SUB(N)
REAL B(N,N) ! 自動割付け配列
!HPF$ DISTRIBUTE B(*,BLOCK)
また、プログラムの部分により、適切な次元数が変化する場合には、 以下のように、割付け配列を利用して、必要に応じて適切な形状の配列を 割り付け、代入文により値を互いに コピーすると良いでしょう。
INTEGER,ALLOCATABLE :: A(:),B(:,:)
!HPF$ DISTRIBUTE A(BLOCK)
!HPF$ DISTRIBUTE B(*,BLOCK)
:
ALLOCATE (A(10000))
:
ALLOCATE (B(100,100))
DO I=1,100
DO J=1,100
B(J,I) = A(J + 100*I)
ENDDO
ENDDO
DEALLOCATE (A)
:
割付け配列は、通常の配列 (ALLOCATABLE属性を持たない配列)
と同様にマップすることができます。
割付け配列の分散と整列を決定する指示文は、その配列の有効域の入り口にお
いて評価され、その有効域で配列が割り付けられる際に使用されます。
割付け配列の利用にあたっては、
割り付けられる実体の整列先となる実体は、必ず存在していなければならない、
ということに注意してください。
次の例で、正しいALLOCATE文の順序を示します。
REAL, ALLOCATABLE :: A(:), B(:)
!HPF$ ALIGN B(I)WITH A(I)
!HPF$ DISTRIBUTE A(BLOCK)
ALLOCATE (A(16))
ALLOCATE (B(16))
上記の例において、配列Aの前に配列Bを割り付けるのは間違いです。
なぜなら、Bが割り付けられたとき、その整列先であるAがまだ割り付けられていないから
です。
INHERIT指示文を仮引数に対して指定すると、対応する実引数のマッピングを そのまま継承することができます。したがって、 DISTRIBUTE指示文、 ALIGN指示文、またはSHADOW指示文を、INHERIT指示文中に記述した仮引数に対して 指定することはできません。
INHERIT指示文により、実引数が様々なマッピングを持つ可能性がある場合に
対応した、汎用的な副プログラムを作成することができますが、
その反面、HPFコンパイラは、翻訳時に
仮引数のマッピングを知ることができないため、
高い実行性能を望むことは難しくなります。
したがって、汎用的なライブラリルーチンをプログラミングするような場合に、
一旦全ての引数をINHERIT指示文を指定して受け取ってから、
HPFライブラリを利用してマッピングを調査した後、
改めて仮引数のマッピングに応じた最適な
副プログラムを引用する、といった用途に適しています。
INHERIT指示文の構文は、付録の INHERIT指示文 の節を参照してください。
HPFには、HPFコンパイラが自動的には最適な並列化が出来ない場合に、
プログラマが情報を与えることで、最適化を促進するための
機能が用意されています。
このような機能は、JAHPFによって策定されたHPF/JA拡張
によって、さらに強化が図られています。
この節では、そのような指示文の利用法を解説します。
INDEPENDENT指示文は、以下のように、繰り返しにまたがる
依存がないループに対して、並列実行可能であることを、
プログラマがHPFコンパイラに明示するための指示文です。
!HPF$ INDEPENDENT
DO I=1,N
A(I) = I
ENDDO
INDEPENDENT指示文の構文は、付録の INDEPENDENT指示文とNEW節、REDUCTION節 の節を参照してください。
INDEPENDENT指示文が指定されたDOループを INDEPENDENT DOループ といいます。
ループの繰り返しにまたがる依存 (データ依存) には、 以下のようなものがあり、 このような依存を含むループは、並列化することができません。
例) 依存: A(I)は、定義された後、引用される
DO I=1,N
A(I) = A(I) + A(I-1)
ENDDO
例) 逆依存: A(I)は、引用された後、定義される
DO I=1,N
A(I) = A(I) + A(I+1)
ENDDO
例) 出力依存: Sは、定義された後、再定義される
DO I=1,N
IF(A(I) > 0.0) S = A(I)
ENDDO
一言で言えば、ある繰り返しで定義されたメモリ領域を 、他の繰り返しで定義あるいは引用すると、 並列化が不可能になります。
HPFコンパイラは、
INDEPENDENT指示文の指定がないDOループに対しても、
翻訳時の解析の結果、依存がないと分かれば、
自動的にINDEPENDENT指示文が指定されたDOループと同様の並列化を
行いますが、ループ中の配列の参照方法によっては、
自動的には最適に並列化できない場合があります。
例えばHPF/ESの場合、
コマンドラインオプション"-Minfo"
により出力される並列化情報で、
あるDOループが、ループの繰り返しにまたがる依存がないにもかかわらず、
INDEPENDENT DOループとして並列化できなかったり、不必要な
通信が生成されたことが分かった場合、
INDEPENDENT指示文を指定することで、
プログラムの実行性能を、劇的に向上させることができる場合もあります。
以下の例の場合、
DO Jのループの左辺と右辺の要素は、重なることがなく、
左辺のG(J,NEW)のマッピングに合わせて、
DO Jのループの各繰り返しを抽象プロセッサへ割り当てると、
シフト転送のみで、効率の良い並列化が可能です。
しかしながら、
現在のところ、
IOLDとINEWの値が常に異なることを解析できないため、
このようなループを
自動的に並列化することができません。
SUBROUTINE INDEP(N,NCYCLES,G)
REAL G(N+2,2)
!HPF$ DISTRIBUTE G(BLOCK,*)
IOLD=1
INEW=2
DO IT =1,NCYCLES
DO J=2,N+1
G(J,INEW)=G(J-1,IOLD)+G(J+1,IOLD)+G(J,IOLD)
ENDDO
IOLD=3-IOLD
INEW=3-INEW
ENDDO
END
実際、 HPF/ESの場合、 コマンドラインオプション"-Minfo"付きで、翻訳を行うと、 以下のようなメッセージが出力されます。
7, Invariant assignments hoisted out of loop
8, Distributing inner loop; 2 new loops
expensive communication: scalar communication (get_scalar)
expensive communication: scalar communication (get_scalar)
このうち、expensive communication: scalar communication (get_scalar)
という2つのメッセージは、オーバヘッドの大きなパタンの
通信が生成されたことを意味しています。
本来必要な通信は、オーバヘッドの少ない
シフト転送のみのはずですから、自動的にはうまく並列化ができなかったことが
分かります。
このような場合、以下のように、DO JのループにINDEPENDENT指示文を
指定すると、
SUBROUTINE INDEP(N,NCYCLES,G)
REAL G(N+2,2)
!HPF$ DISTRIBUTE G(BLOCK,*)
IOLD=1
INEW=2
DO IT =1,NCYCLES
!HPF$ INDEPENDENT
DO J=2,N+1
G(J,INEW)=G(J-1,IOLD)+G(J+1,IOLD)+G(J,IOLD)
ENDDO
IOLD=3-IOLD
INEW=3-INEW
ENDDO
END
コマンドラインオプション"-Minfo"付きで、翻訳したときのメッセージが 以下のようになり、 オーバヘッドの高い通信なしで、うまく INDEPENDENTループが並列化され たことが分かります。
7, Invariant communication calls hoisted out of loop
9, Independent loop parallelized
以下で述べるように、 INDEPENDENT指示文を指定するためには、 NEW節 や REDUCTION節 を同時に指定しなければならない場合もあります。
INDEPENDENT DOループが並列化されない 原因として、 以下の例の配列Aのように、 ループ中で定義されている配列が、 複数個所で参照されている場合が挙げられます。
INTEGER A(N),B(N),J1(N),J2(N)
!HPF$ DISTRIBUTE (BLOCK) :: A,B,J1,J2
!HPF$ INDEPENDENT,NEW(I)
DO I = 1,N
A(J1(I)) = B(I)
A(J2(I)) = 1
ENDDO
この例で、DOループが配列Bに合わせて並列化され、
最初の配列Aへの参照が一時配列A_TMP1に置き換わり、
2番目のものが一時配列A_TMP2に置き換わるとすると、
ループ実行後に、
一時配列の値をAに書き戻すとき、
HPFコンパイラはどちらの一時配列の値をループ後の値として採用して良いかを
決定できません。
このような場合は、2つの代入文を別のループに分割して
記述するか、もし可能な場合は、LOCAL節中に配列Aを記述したON指示文
を指定することにより、並列化が可能になります。
(
ON指示文
と、
LOCAL節
の節を参照してください。
)
ある変数に対して、複数の繰り返しで値が代入される場合、ループの繰り返し
にまたがる依存関係を持つことになり、並列化の阻害要因となります。
しかし、もしこのような変数が、ループの1つの繰り返し中に閉じた
作業変数として使われており、ループの繰り返し間で値を伝達したり、
ループ実行後に値が引用されたりすることがない場合、
そのような変数をNEW節に指定すれば、INDEPENDENT指示文を
指定することができます。
NEW節中に指定された変数を
NEW変数
と言います。
NEW変数は、HPFコンパイラにより、
INDEPENDENT DOループの各繰り返し毎に新しい一時領域
が生成されるかのように扱われ、依存関係がないものとみなされます。
次のコードは、INDEPENDENT指示文指定の際に、NEW節が必要な例を示しています。
DO I = 1,N
S = SQRT(A(I)**2 + B(I)**2)
C(I) = S
ENDDO
このループで、Sは、各繰り返しのはじめに、計算結果を
一時格納するために定義された後、引用されています。
NEW節なしで、このDOループにINDEPENDENT指示文を指定するためには、
各繰り返しで定義/引用されるメモリ領域を
別々のものにするため、以下のように、Sを配列化しなければなりません。
!HPF$ INDEPENDENT
DO I = 1,N
S(I) = SQRT(A(I)**2 + B(I)**2)
C(I) = S(I)
ENDDO
しかし、NEW節を利用して、以下のように指定すれば、 Sは、HPFコンパイラにより、ループの各繰り返し中に閉じた作業変数として 扱われ、上記のようなプログラムの書き換えをする必要がありません。
!HPF$ INDEPENDENT, NEW(S)
DO I = 1,N
S = SQRT(A(I)**2 + B(I)**2)
C(I) = S
ENDDO
ただし、NEW変数の値は、INDEPENDENT DOループの実行後、不定となります。
したがって、ループ実行後、
NEW変数 (この場合は、S) に値を代入することなくそのまま引用した場合、
プログラムの動作は保証されません。
特に、INDEPENDENT DOループ中に内包されるDOループのDO変数は、
INDEPENDENT DOループの各繰り返しで値が代入されることになるため、
NEW変数である必要があり、したがって、INDEPENDENT DOループの実行後に
値を代入することなくそのまま引用した場合、プログラムの動作は保証されない
ことに注意してください。
例えば、以下の例では、INDEPENDENT DOループであるDO Iのループ
に含まれるDO JのループのDO変数Jを、NEW節中に指定する必要があり、
INDEPENDENT DOループ実行後に、Jの値は不定となります。
!HPF$ INDEPENDENT,NEW(I,J)
DO I=1,N
DO J=1,N
A(J,I) = A(J-1,I)
ENDDO
ENDDO
ここで、最外側INDEPENDENT DOループのDO変数Iの、NEW節中への指定は、 Iがループ実行後にとる値N+1を保証するためのオーバヘッドが 削減される効果を持ちます。
例えば
HPF/ESの場合、
INDEPENDENT DOループとして並列化可能かどうかの
解析をする際には、NEW変数も自動的に検出します。
ただし、現在のところ、配列が作業変数として利用されている場合には、
自動検出ができないので、そのようなループを効率よく
並列化するためには、NEW節を含むINDEPENDENT指示文を指定する必要があります。
例えば、以下のコードでは、配列Fの分散次元に対応するDO Kのループで、
通信の必要なく並列化することができます。
ところが、このループ中では、配列U、FLUXが、作業変数として利用されており、
各繰り返し毎に、定義されては、引用されています。
SUBROUTINE RHS(F,U,N1,N2,N3)
COMMON /COM/C1,C2,Q
DIMENSION FLUX(2,N1),U(2,N1)
DIMENSION F(2,N1,N2,N3)
!HPF$ DISTRIBUTE F(*,*,*,BLOCK)
DO K=2,N3-1
DO J=2,N2-1
DO I=1,N1
DO M=1,2
U(M,I) = C1 - C2
ENDDO
FLUX(1,I) = Q * U(1,I)
FLUX(2,I) = Q * U(2,I)
ENDDO
DO I=2,N1-1
F(1,I,J,K) = F(1,I,J,K) * (FLUX(1,I+1)-FLUX(1,I-1))
F(2,I,J,K) = F(2,I,J,K) * (FLUX(2,I+1)-FLUX(2,I-1))
ENDDO
ENDDO
ENDDO
END
HPF/ESの場合、 このコードを、 コマンドラインオプション"-Minfo"付きで翻訳すると、 以下のようなメッセージが出力されます。
9, Distributing loop; 2 new loops
1 FORALL generated
2 FORALLs generated
no parallelism: replicated array, u
no parallelism: replicated array, flux
no parallelism: replicated array, flux
10, Independent loop
16, Independent loop
2 FORALLs generated
10, Independent loop、16, Independent loopにより、
10行目のDO Mのループおよび16行目のDO Iのループは、INDEPENDENT DO
ループであると判定されていることが分かりますが、
肝心のDO Kのループは、INDEPENDENT DOループとは
認識されなかったことが分かります。
そこで、以下のように、明示的にNEW節付きのINDEPENDENT指示文
を指定すれば、
SUBROUTINE RHS(F,U,N1,N2,N3)
COMMON /COM/C1,C2,Q
DIMENSION FLUX(2,N1),U(2,N1)
DIMENSION F(2,N1,N2,N3)
!HPF$ DISTRIBUTE F(*,*,*,BLOCK)
!HPF$ INDEPENDENT,NEW(K,I,J,M,U,FLUX)
DO K=2,N3-1
DO J=2,N2-1
DO I=1,N1
DO M=1,2
U(M,I) = C1 - C2
ENDDO
FLUX(1,I) = Q * U(1,I)
FLUX(2,I) = Q * U(2,I)
ENDDO
DO I=2,N1-1
F(1,I,J,K) = F(1,I,J,K) * (FLUX(1,I+1)-FLUX(1,I-1))
F(2,I,J,K) = F(2,I,J,K) * (FLUX(2,I+1)-FLUX(2,I-1))
ENDDO
ENDDO
ENDDO
END
コマンドラインオプション"-Minfo"による HPF/ESの 出力は、 以下のようになり、8行目のDO KのループがINDEPENDENT DOループとして 並列化されたことが分かります。
8, Independent loop parallelized
11, Independent loop
17, Independent loop
複数のINDEPENDENT DOループが入れ子になっている場合、NEW変数の
NEW節への指定場所は、そのNEW変数に定義を行う
ようなINDEPENDENT DOループの内、一番内側です。
例えば、以下の例の場合、IおよびJのINDEPENDENT DOループ中で
代入される作業変数Sは、最内側のDO Jのループに対するINDEPENDENT
指示文のNEW節中に記述します。
!HPF$ INDEPENDENT, NEW(I,J)
DO I = 1,N
!HPF$ INDEPENDENT, NEW(S)
DO J = 1,N
S = SQRT(A(I,J)**2 + B(I,J)**2)
C(I,J) = S
ENDDO
ENDDO
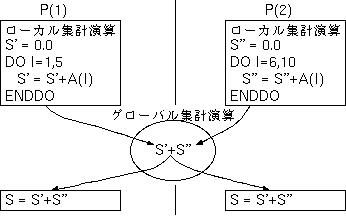
以下のように、ある特定の変数(この場合はS)に、ループの各繰り返しで 次々と同じ種類の演算が行われ、その値が蓄積されていく場合、 ループの繰り返し間での依存があることになるため、そのままでは、 INDEPENDENT指示文を指定することはできません。
REAL A(10)
!HPF$ PROCESSORS P(2)
!HPF$ DISTRIBUTE A(BLOCK) ONTO P
S=0
DO I = 1,10
S = S + A(I)
ENDDO
しかし、加法には結合律と交換律が成立しますから、 Aの要素を足し込む順序の違いに起因する丸め誤差 を許容できるならば、 各抽象プロセッサが、まず 配列Aの所有範囲の部分だけを一時領域に足し込んでおき (これを、 ローカル集計演算 と言います) 、 その後、それぞれの計算結果を通信を行って足し合わせる (これを、 グローバル集計演算 と言います) ことにより、以下のように、並列実行を行うことができます。
|
この例のSのような変数を、 以下のように、REDUCTION節中に記述することによって、 INDEPENDENT指示文を指定することが可能になります。 REDUCTION節中に記述された変数を、 集計変数 と言います。
REAL A(10)
!HPF$ DISTRIBUTE A(BLOCK)
S=0
!HPF$ INDEPENDENT, REDUCTION(S)
DO I = 1,10
S = S + A(I)
ENDDO
NEW節中に集計変数を指定するのは、 集計変数の値がループの繰り返し間で蓄積されなければならず、さらに、 ループ実行後に値が保存されていなければならないことから間違いです。
集計変数は、INDEPENDENT DOループ中で、以下のような特定の形式の代入文 にしか、記述することができません。これらの文を 集計文 と言います。
A = A + E
A = E + A
A = A - E
A = A * E
A = E * A
A = A / E
A = A .or. E
A = A .and. E
A = A .eqv. E
A = A .neqv. E
A = iand(A, E1,..., En)
A = ior(A, E1,..., En)
A = ieor(A, E1,..., En)
A = min(A, E1,..., En)
A = max(A, E1,..., En)
これら集計文中で、AはREDUCTION節中の集計変数 (上記の例ではS) であり、 E,E1,...,EnはAを含まない式とします。 また上記の右辺中の演算子は、右辺の式中で、最後に実行される 演算子でなければなりません。
複数のINDEPENDENT DOループが入れ子になっている場合、集計変数の REDUCTION節への指定場所は、その変数に対する集計演算を含む INDEPENDENT DOループの内、一番外側です。 例えば、以下の例の場合、IおよびJのINDEPENDENT DOループ中で、集計演算が行われる 集計変数Sは、最外側のDO Iのループに対するINDEPENDENT指示文の REDUCTION節中に記述します。
!HPF$ INDEPENDENT, NEW(I),REDUCTION(S)
DO I = 1,N
!HPF$ INDEPENDENT, NEW(J)
DO J = 1,N
S = S + A(I,J)
ENDDO
ENDDO
HPFコンパイラ は、各抽象プロセッサ上にマップされる配列の部分を、 マップされた配列のメモリレイアウト の図のように、 Fortranと同様の配列要素順序に 基づいてメモリ上に割り付けます。
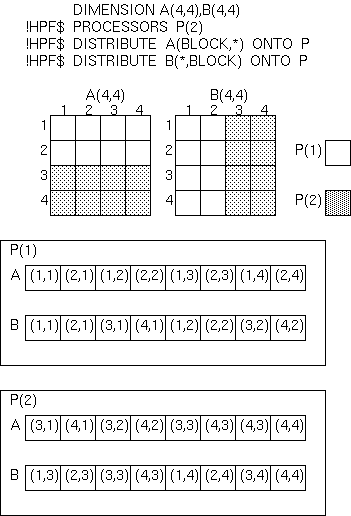
|
そのため、Fortranの場合と同様に、 低い次元をアクセスするループを内側に した方が、メモリ上のアクセスが連続になるため、 より効率の良い実行が可能です。
! 低い次元をアクセスするループが内側
DO I=1,N
DO J=1,N
A(J,I) =
! 低い次元をアクセスするループが外側
DO J=1,N
DO I=1,N
A(J,I)
以下の例において、最初のループネストでは、 配列A、Bのマップされた次元 (2次元目) が、 外側のDO Iのループでアクセスされているのに対して、 2番目のループでは、配列C、Dのマップされた次元 (1次元目) が内側のDO Jのループでアクセスされています。
PARAMETER (N=1000)
DIMENSION A(N,N),B(N,N)
!HPF$ DISTRIBUTE (*,BLOCK) :: A,B
DIMENSION C(N,N),D(N,N)
!HPF$ DISTRIBUTE (BLOCK,*) :: C,D
DO I=1,N
DO J=1,N
A(J,I)=B(J,I)
ENDDO
ENDDO
DO I=1,N
DO J=1,N
C(J,I)=D(J,I)
ENDDO
ENDDO
どちらのループネストも、
並列化そのものは、DO I、DO Jいずれのループでも可能ですが、
マップされていない次元に対応するループで並列化すると、
リモートアクセスが発生するため、
例えば
HPF/ESの場合、
最初のループネストに関しては、
外側のDO Iのループのみを、
2番目のループネストに関しては、
内側のDO Jのループのみを並列化します。
一般的に、
外側のループで並列化された方が、並列化の粒度を大きくし易いため、
並列化のためのオーバヘッドの総量も少なくなる確率が高くなります。
そのため、アルゴリズム上問題がないのであれば、
外側の並列ループに対応する次元でマップした方が、良い場合が多いでしょう。
逆に、マップされた配列にアクセスするループを記述する際には、 マップされた次元に対応する並列ループを外側にした方が良い 場合が多いでしょう。
HPFコンパイラは、
基本的には、INDEPENDENT指示文が指定されたDOループネスト、
および
HPFコンパイラが
INDEPENDENTであると判定したDOループネスト
を1つの単位として並列化を行います。
そのため、1つのループネストは、できるだけ
リモートアクセスが生じないように構成した方が
高い性能が期待できます。
例えば HPF/ESの場合、 以下の例における、DO IとDO Jのループは、 自動的にINDEPENDENTであると判定されますが、 DO Jのループは、配列のマップされた次元に対応していないので 並列化されず、 配列B、Cのマップされた次元に対応している DO Iのループだけが並列化されます。
SUBROUTINE SUB(A,B,C,N)
DIMENSION A(N,N),B(N,N),C(N,N)
!HPF$ DISTRIBUTE (*,BLOCK) :: B,C
DO I=1,N
B(I,I) = C(I,I)
DO J=1,N
A(I,J)=I*1.0D0
ENDDO
ENDDO
END
ところが、配列Aはマップされていないので、
DO Iの各繰り返しにおいて定義されたAの値を、他のプロセッサに反映するための
リモートアクセスが必要となり、通信が生成されます。
実際、上記のコードを、HPF/ESにより、
コマンドラインオプション"-Minfo"を指定して翻訳すると、
以下のようなメッセージが出力されます。
5, Independent loop
Array a not aligned with home array; array copied
Independent loop parallelized
no parallelism: replicated array, a
7, Independent loop
"5, Independent loop"、"7, Independent loop"の2行から、
5行目のDO Iのループ、および7行目のDO Jのループが、自動的に
INDEPENDENTであると判定されたことが分かりますが、
"Array a not aligned with home array; array copied"
という行から、5行目のDO Iのループの並列化の際に、
配列Aに対する通信が生成されたことが分かります。
このような場合、以下のように、各繰り返しで
アクセスされる要素が、同一の抽象プロセッサ上にマップされる
ようにDOループを分割すると、
通信なしで並列実行が可能となり、実行性能が向上します。
SUBROUTINE SUB(A,B,C,N)
DIMENSION A(N,N),B(N,N),C(N,N)
!HPF$ DISTRIBUTE (*,BLOCK) :: B,C
DO I=1,N
B(I,I) = C(I,I)
ENDDO
DO I=1,N
DO J=1,N
A(I,J)=I*1.0D0
ENDDO
ENDDO
END
実際、 HPF/ESの場合、 上記のコードに対して、コマンドラインオプション"-Minfo"により 出力されるメッセージは以下のようになり、 通信の生成なしで並列化されたことが分かります。
5, Independent loop
Independent loop parallelized
9, Independent loop
10, Independent loop
逆に、以下のように、各繰り返しでアクセスされる 要素が、同一の抽象プロセッサ上にマップされているような ループネストが複数連続する場合には、
DIMENSION A(N,N),B(N,N),C(N,N)
!HPF$ DISTRIBUTE (*,BLOCK) :: A,B,C
DO I=1,N
DO J=1,N
A(J,I)=B(J,I)
ENDDO
ENDDO
DO I=1,N
DO J=1,N
C(J,I)=B(J,I)
ENDDO
ENDDO
以下のように、一つのループに融合した方が、 並列化のためのオーバヘッドが少なくなります。
DIMENSION A(N,N),B(N,N),C(N,N)
!HPF$ DISTRIBUTE (*,BLOCK) :: A,B,C
DO I=1,N
DO J=1,N
A(J,I)=B(J,I)
C(J,I)=B(J,I)
ENDDO
ENDDO
HPFコンパイラは、
FORALL文と配列代入文を、
オーナーコンピュートルールに基づいて、
並列化します。
オーナーコンピュートルール
とは、
ある文で定義される
要素がマップされている抽象プロセッサに、その文の処理を
割り当てる計算マッピングの手法です。
例えば以下の配列代入文では、定義される配列A
の所有範囲に合わせて、計算マッピングが行われます。
A(1:N) = B(1:N)
FORALL構文は、FORALL文が複数連続に記述された場合と同様に 扱われ、FORALL構文中の代入文が、それぞれ独立に 並列化されます。
HPFコンパイラは、
並列化されたFORALL文や配列代入文が連続している場合、
可能な限り融合して、並列化の粒度をあげようと試みますが、
ループの上下限、配列のマッピングやアクセス方法の違いなどにより、
融合できない場合もあります。
一括して並列化したい処理は、
FORALL文や配列代入文ではなく、
DOループによって、明示的に一つのループネストにまとめて書いた方が、
並列化の粒度をあげやすくなります。
一般に、手続の引用を含むDOループは、翻訳時には、 並列化可能かどうかが不明であるめ、 組込みサブルーチン(例えば、randum_number()) や、PUREでない手続の引用は、 INDEPENDENT DOループの並列化を妨げます。
PURE手続を含むINDEPENDENT DOループを並列化することは可能ですが、 この場合、プログラマは、ループに対してINDEPENDENT指示文を 指定した上で、明示的引用仕様により、引用される手続がPUREであることを 明示する必要があります。
以下の例では、サブルーチンSUBを 1度呼び出すたびに、2次元配列Aの各列を引数として渡して、 値を設定していますが、 各繰り返しで引数以外の 変数の値が変ったり、入出力を行ったりしないので、 並列に実行することが可能です。
INTEGER A(100,100)
!HPF$ DISTRIBUTE A(*,BLOCK)
DO I=1,100
CALL SUB(A(:,I))
ENDDO
:
SUBROUTINE SUB(A)
INTEGER A(100)
DO I=1,100
A(I) = I
ENDDO
END
例えば HPF/ESの場合、 以下のような手順により、
INDEPENDENT指示文を指定することができ、 HPF/ESは、 DO Iのループの各繰り返しを、Aの所有範囲に合わせて、 抽象プロセッサに分配します。
INTEGER A(100,100)
!HPF$ DISTRIBUTE A(*,BLOCK)
INTERFACE
PURE SUBROUTINE SUB(A)
INTEGER A(100)
INTENT(OUT) :: A
END SUBROUTINE
END INTERFACE
!HPF$ INDEPENDENT
DO I=1,100
CALL SUB(A(:,I))
ENDDO
:
PURE SUBROUTINE SUB(A)
INTEGER A(100)
DO I=1,100
A(I) = I
ENDDO
END
PURE手続とHPF指示文に関する詳細は、
High Performance Fortran Language Specification
November 10, 1994 Version 1.1 の 4.3 節を
を参照してください。
特に、PURE手続を実行する抽象プロセッサは、
HPFコンパイラが自動的に決定するため、
PURE手続内では、DISTRIBUTE指示文によって、
データの抽象プロセッサへの分散を直接指定してはならない、ということに
注意してください。
ON指示文は、各文を実行する抽象プロセッサを、プログラマが指定するための 指示文です。 ON指示文により指定された抽象プロセッサを 活動プロセッサ と言います。 ON指示文の対象となる一連の文の集合を ONブロック と言います。
HPFコンパイラが INDEPENDENT DOループを並列化する場合、 一つのマップされた配列を基準として、各抽象プロセッサが、 基準配列の所有部分だけを アクセスするように、ループの繰り返しを各抽象プロセッサに 振り分けますが、このような基準配列を ホーム配列 と言います。 ON指示文によって、ホーム配列を明示的に指定することができます。
ON指示文の最も有効な利用方法は、
後の節で述べるREFLECT指示文やLOCAL節と併用して、リモートアクセスの必要なく
実行可能な計算マッピングを明示することにより、通信を削減することです。
利用例に関しては、
LOCAL節
の節を参照してください。
ON指示文の構文は、付録の ON指示文とLOCAL節 の節を参照してください。
ON指示文と共に、LOCAL節を指定することにより、
ON指示文で指定された計算マッピングに従うと、
リモートアクセスなしで実行が行えることを
明示することができます。
ここで、リモートアクセスかローカルアクセスかの判断は、
その文を実行する抽象プロセッサが決定されて初めて可能になるため、
LOCAL節の利用には、ON指示文が必要であることに
注意してください。
例えば、以下のような処理は、配列の境界処理によく出現しますが、 DO Iのループに対応するAの1次元目はマップされていないため、 ループ処理全体をA(:,1)がマップされている抽象プロセッサ に割り当てるのが最適です。
REAL A(N,N)
!HPF$ DISTRIBUTE A(*,BLOCK)
DO I=1,N
A(I,1) = A(I,1) + A(I+1,1)
ENDDO
以下のように、Aに対するLOCAL節付きのON指示文を指定することにより、 通信なしで、ループ全体の実行をA(:,1)がマップされた抽象プロセッサ上で 実行させることができます。
REAL A(N,N)
!HPF$ DISTRIBUTE A(*,BLOCK)
!HPF$ ON HOME(A(:,1)),LOCAL(A)
DO I=1,N
A(I,1) = A(I,1) + A(I+1,1)
ENDDO
次の例は、スパース行列処理で良く用いられる データ構造を示しています。
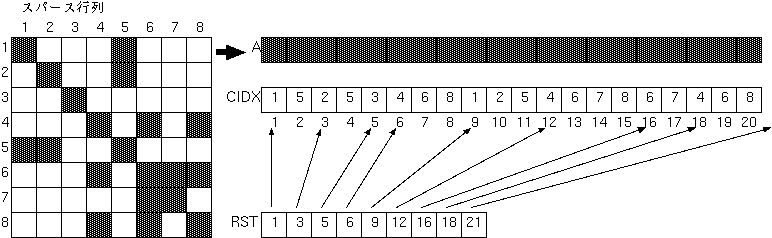
|
ここで、1次元配列Aには、スパース行列の非零要素の値だけが
圧縮された形て設定されています。
1次元配列CIDXには、非零要素の列番号がやはり圧縮された
状態で設定されており、
RST(I)には、第I行目の非零要素に
対応するCIDX、Aの要素のうち、最初の要素の添字値が
設定されています。
次のコードは、このようなデータ構造をもつ
スパース行列に関する行列ベクトル積の例です。
SUBROUTINE SUB(NNZ,N)
REAL A(NNZ),B(N),X(N)
INTEGER CIDX(NNZ),RST(N+1)
:
DO I=1, N
B(I) = 0.0
DO J = RST(I),RST(I+1)-1
B(I) = B(I) + A(J) * X(CIDX(J))
ENDDO
ENDDO
このようなループを、例えば3つの抽象プロセッサで 並列実行したい場合、以下のようにマップすれば、 通信の必要なく、Iのループを並列化することができます。
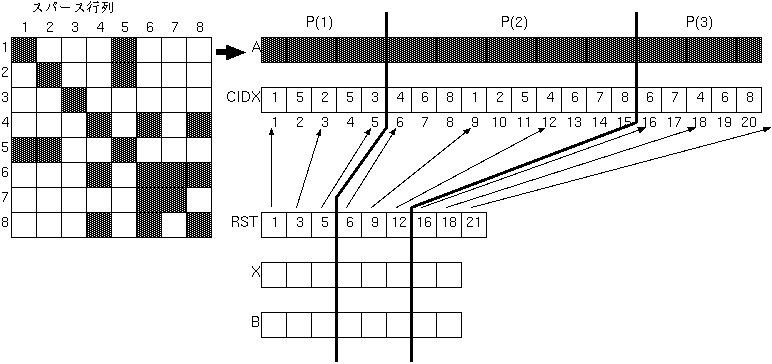
|
ただし、マッピングの指定だけでは、
A(J)、CIDX(J) および X(CIDX(J))のアクセスの際、
リモートアクセスが発生しないことを、
自動的に検出することができないので、
LOCAL節付きのON指示文を指定する必要があります。
結局、以下のようにデータマッピングと計算マッピングを指定すれば、
通信オーバヘッドなしに、DO Iのループを並列実行することができます。
PARAMETER (N=8,NNZ=20)
INTEGER GB(3)
GB = (/5,10,5/)
CALL SUB(NNZ,N,GB)
END
SUBROUTINE SUB(NNZ,N,GB)
REAL A(NNZ),B(N),X(N)
INTEGER CIDX(NNZ),RST(N+1)
INTEGER GB(3)
!HPF$ DISTRIBUTE (GEN_BLOCK(GB)) :: A,CIDX
!HPF$ DISTRIBUTE (BLOCK) :: RST
!HPF$ ALIGN (I) WITH RST(I) :: B,X
:
DO I=1, N
!HPFJ ON HOME(B(I)), LOCAL(A,CIDX,X) BEGIN
B(I) = 0.0
DO J = RST(I),RST(I+1)-1
B(I) = B(I) + A(J) * X(CIDX(J))
ENDDO
!HPFJ ENDON
ENDDO
LOCAL節の構文は、付録の ON指示文とLOCAL節 の節を参照してください。
宣言部でSHADOW指示文を指定した配列に対して、
REFLECT指示文を指定すれば、
そのシャドウ領域に、対応するデータ実体の値を設定することができます。
典型的には、REFLECT指示文で設定したシャドウ実体の値を、
LOCAL節を持つON指示文中で、通信なしに参照することにより、
これらの機能なしでは複数回実行される通信を一度にまとめる、といった
HPFコンパイラが自動的にはできない最適化を行うことができます。
例えば、以下のコードにおいて、2つのループを、Aをホーム配列として並列実行する
場合、配列Bに対してシフト転送が必要となります。
ここで、2つのループの間に、配列Bが定義されるような処理がない場合、
最初のループの直前にシフト転送を行えば、
2番目のループ中では、Bのシャドウ領域の値を
そのまま再利用することができるため、
2番目のループの実行時には、
シフト転送を省略することができます。
REAL A(100),B(100)
!HPF$ DISTRIBUTE (BLOCK) :: A,B
!HPF$ ALIGN B(I) WITH A(I)
:
DO I=1, 99
A(I) = A(I)+B(I+1)
ENDDO
:
DO I=1, 99
A(I) = A(I)+B(I+1)
ENDDO
例えば
HPF/ESの場合、
通常は、自動的にこのような通信の融合を行いますが、
2つのループの間に手続引用がある等の理由で、
各ループの直前にそれぞれシフト転送を生成する場合があります。
そのような場合でも、もし2つのループ間で、Bの値が変化しない
ことをプログラマが分かっている場合には、
以下のように、
シフト転送の回数を1度だけに押さえることができます。
REAL A(100),B(100)
!HPF$ DISTRIBUTE (BLOCK) :: A,B
!HPF$ ALIGN B(I) WITH A(I)
!HPF$ SHADOW B(0:1)
:
!HPFJ REFLECT B
DO I=1, 99
!HPFJ ON HOME(A(I)),LOCAL(B)
A(I) = A(I)+B(I+1)
ENDDO
:
CALL SUB(B)
:
DO I=1, 99
!HPFJ ON HOME(A(I)),LOCAL(B)
A(I) = A(I)+B(I+1)
ENDDO
以下の例では、DO Jのループを、Aをホーム配列として並列実行する場合、
配列Bに対してシフト転送が必要となります。
もし、外側のDO Iのループ中に配列Bの定義がないならば、
シフト転送は、DO Jループの実行直前に毎回行う必要はなく、
外側のDO Iのループの実行直前に一度だけ行えば十分です。
例えば
HPF/ESの場合、
可能な限り自動的にこのような通信のループ外への
括り出しを行いますが、
DO Iのループ中に手続引用がある場合などは、副作用の可能性があるため、
常にこのような最適化が可能とは限りません。
REAL A(100),B(100)
!HPF$ DISTRIBUTE (BLOCK) :: A,B
...
DO I=1,N ! 並列化できないループ
...
DO J=1, 99
A(J) = A(J) + B(J+1)
ENDDO
...
ENDDO
HPFコンパイラが、 自動的には、通信のループ外への括り出しができない場合でも、 以下のように、
HPFコンパイラに対して、シフト転送を最良の場所である外側のDO Iのルー プ直前で行うように指示することができます。
REAL A(100),B(100)
!HPF$ DISTRIBUTE (BLOCK) :: A,B
!HPF$ SHADOW B(0:1)
...
!HPFJ REFLECT B
DO I=1,N
...
!HPF$ INDEPENDENT,NEW(J)
DO J=1, 99
!HPFJ ON HOME(A(J)), LOCAL(B)
A(J) = A(J)+B(J+1)
ENDDO
...
CALL SUB(B)
...
ENDDO
次の例においては、そのままでは、 シャドウ領域 内に、 シフト転送に必要な幅Nが 含まれるかどうか分からないため、 オーバヘッドの小さいシフト転送ではなく、 よりオーバヘッドの大きい通信が、配列Aに対して生成されます。
SUBROUTINE SUB(A,B,N)
REAL A(100),B(100)
!HPF$ DISTRIBUTE (BLOCK) :: A,B
...
!HPF$ INDEPENDENT,NEW(I)
DO I=2, 99
B(I) = A(I) + A(I+N)
ENDDO
もし、プログラマが、Nの値が1、または-1であることを知っている場合には、 以下のように、SHADOW指示文、REFLECT指示文、 およびAをLOCAL節中に記述したON指示文を指定することにより、 HPFコンパイラに対してオーバヘッドの小さいシフト転送だけで、 並列処理を行うよう指示することができます。
SUBROUTINE SUB(A,B,N)
REAL A(100),B(100)
!HPF$ DISTRIBUTE (BLOCK) :: A,B
!HPF$ SHADOW A(1)
...
!HPFJ REFLECT A
!HPF$ INDEPENDENT,NEW(I)
DO I=2, 99
!HPFJ ON HOME(B(I)),LOCAL(A)
B(I) = A(I) + A(I+N)
ENDDO
REFLECT指示文の構文は、付録の REFLECT指示文 の節を参照してください。
ここでは、特に、有限要素法やスパース行列処理に出現するような 不規則なアクセスパタンを持つ問題に適したHPFの機能に関して述べます。
HPF/JA1.0仕様で定義されているINDEX_REUSE指示文は、 以下のように間接アクセス を含む処理が何度も繰り返される場合に、前回の実行時と間接アクセス添字の 値が全く同じであることをHPFコンパイラに明示するための 指示文です。
DO IT =1 NCYCLE ! 繰り返し
...
!HPFJ INDEX_REUSE ( 論理式 ) A
DO I= ...
... A(IDX(I))... ! 間接アクセス
ENDDO
...
ENDDO
INDEX_REUSE指示文の構文は、付録の INDEX_REUSE指示文 の節を参照してください。
HPFコンパイラは、INDEX_REUSE指示文の指定があると、 最初の実行時の添字情報を保存しておくことができ、 2回目以降の実行時に、通信や参照のための情報を再利用することにより、 最初の実行時のオーバヘッドを償却していくことができます。
HPF2.0公認拡張のINDIRECT分散により、 各配列要素がマップされる抽象プロセッサ番号を直接指定することで、 不規則なマッピングを表現することができます。
!HPF$ PROCESSORS P(4)
REAL A(100)
INTEGER map1(100)
PARAMETER (map1=(/1,3,4,3,3,2,1,4,...,/))
!HPF$ DISTRIBUTE A(INDIRECT(map1)) ONTO P
INDIRECT分散を利用することで、不規則問題に対して、
少ない手間で、HPFプログラムを開発することが可能です。
しかし、
INDIRECT分散のマッピング配列は、分散対象となる主要配列の
寸法と同じ大きさが必要となることや、INDIRECT分散された配列
をアクセスする際に必要なアドレス変換のオーバヘッドが大きいこと
から、効率の良い分散とは言えません。
(アドレス変換に関しては、
CYCLIC分散とアドレス変換
の節を参照してください。)
一般的には、対象配列の添字を昇順に並び替えることが可能なら、
GEN_BLOCK分散を利用する方が、実行性能やメモリ利用効率の点では、
優れていると言えます。
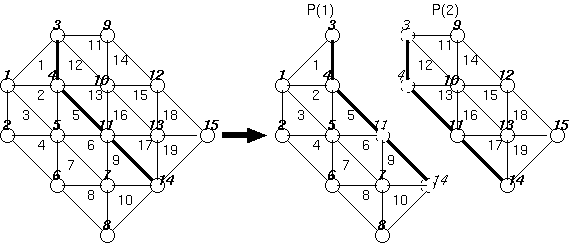
例えば、以下のようなマッピングは、
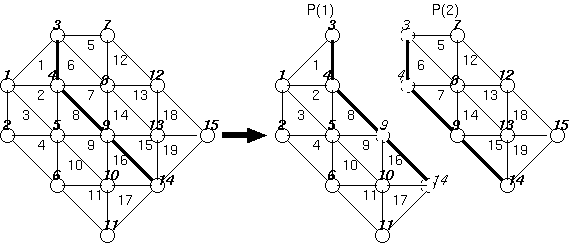
|
INDIRECT分散を利用して、以下のように記述することができます。
PARAMETER (NUM_PE = 2) ! 抽象プロセッサ数
PARAMETER (NNODE = 15, NELM=19) ! ノード数、要素数
INTEGER ID_NODE(NNODE),ID_ELM(NELM)
DATA ID_NODE /1,1,1,1,1,1,2,2,2,1,1,2,2,2,2/
DATA ID_ELM /1,1,1,1,2,2,2,1,1,1,1,2,2,2,2,1,1,2,2/
REAL NODE(NNODE),ELM(NELM)
!HPF$ PROCESSORS P(NUM_PE)
!HPF$ DISTRIBUTE NODE(INDIRECT(ID_NODE)) ONTO P
!HPF$ DISTRIBUTE ELM(INDIRECT(ID_ELM)) ONTO P
ここで、もし、各ノードや要素の番号づけが重要ではない場合、 番号の付け替え の図のように、 番号を付け替えるだけで、 各ノードや要素が、どの抽象プロセッサにマップされるかは、 全く変化しないにも関わらず、 GEN_BLOCK分散が利用できることに注意してくだ さい。
|
外来手続は、HPFから、HPF以外の手続を引用するための機能です。
HPFから、外来手続を引用する場合、 明示的引用仕様が必要です。
通常のHPF手続が、
グローバルモデル
であるのに対して、
HPF_LOCAL手続は、HPFで記述された
ローカルモデル (
SPMDモデル) の手続です。
グローバルモデル
のHPF手続の場合、
HPFコンパイラが、計算マッピングや必要な通信の生成を行い、
SPMDモデルの中間ソースを生成するのに対して、
HPF_LOCAL手続では、プログラマが、直接SPMDモデルに
基づいたプログラムを記述し、HPFコンパイラは、
計算マッピングや通信の生成などは一切行いません。
HPF_LOCAL手続を利用することにより、 手続の並列起動を容易に記述することができ、 また、HPFコンパイラには困難なチューニングを行うことができます。
例えば、以下の例は、 INDEPENDENT DOループ中の手続引用 の節で述べた、PURE手続による手続引用の並列化の例ですが、
INTEGER A(100,100)
!HPF$ DISTRIBUTE A(*,BLOCK)
INTERFACE
PURE SUBROUTINE SUB(A)
INTEGER A(100)
INTENT(OUT) :: A
END SUBROUTINE
END INTERFACE
!HPF$ INDEPENDENT
DO I=1,100
CALL SUB(A(:,I))
ENDDO
:
PURE SUBROUTINE SUB(A)
INTEGER A(100)
DO I=1,100
A(I) = I
ENDDO
END
同様の処理を、次のような手順により、
HPF_LOCAL手続を利用して記述すると、 以下のようになります。
INTEGER A(100,100)
!HPF$ DISTRIBUTE A(*,BLOCK)
INTERFACE
EXTRINSIC(HPF_LOCAL) SUBROUTINE SUB(A)
INTEGER A(:,:)
!HPF$ DISTRIBUTE A(*,BLOCK)
END SUBROUTINE
END INTERFACE
CALL SUB(A)
:
EXTRINSIC(HPF_LOCAL) SUBROUTINE SUB(A)
INTEGER A(:,:)
DO J=1,UBOUND(A,2)
DO I=1,UBOUND(A,1)
A(I,J) = I
ENDDO
ENDDO
END
この場合、各抽象プロセッサは、それぞれ独立に、
HPF_LOCAL手続であるサブルーチンSUBを起動し、
明示的引用仕様中で指定されたマッピングにしたがって、
ローカルアクセス可能な配列部分を対象に、サブルーチンSUB中
の処理を実行することになります。
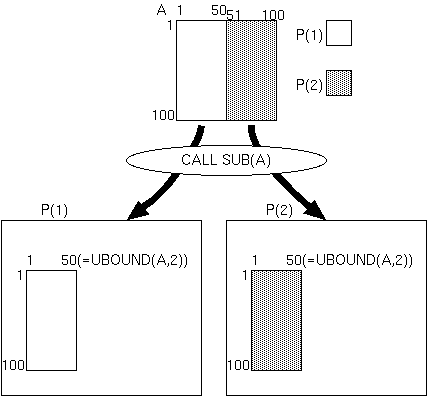
例えば、上記のプログラムを、P(1)、P(2)の2つの抽象プロセッサ上で
実行した場合、以下のように、
P(1)は、呼出元のグローバル手続におけるA(1:100,1:50)に対応する
ローカル配列A(1:100,1:50)に対して、サブルーチンSUBを実行し、
P(2)は、呼出元のグローバル手続におけるA(1:100,51:100)に対応する
ローカル配列A(1:100,1:50)に対して、サブルーチンSUBを実行することになります。
|
ここで、グローバルモデルのHPF手続から引用されるHPF_LOCAL手続の
仮引数がマップされている場合、
形状引継配列として宣言しなければなりません。
形状引継配列の下限は、省略された場合1であるため、
抽象プロセッサP(2)上においては、呼出元のグローバルモデル
HPF手続におけるローカルな要素の添字の範囲
と、HPF_LOCAL手続
におけるローカル配列の上下限の値が異なることに注目してください。
このように、グローバルモデルの手続における添字値と、
ローカルモデルの手続における対応する要素の添字値は、
一般に異なることに注意する必要があります。
また、Fortranの組込み手続LBOUND、UBOUNDは、
グローバルモデル手続中とローカルモデル手続中では
一般に、異なる値を返します。
例えば、上記の例では、LBOUND、UBOUNDの値は、それぞれ以下のようになります。
| グローバルモデル | ローカルモデル | ||
|---|---|---|---|
| P(1)、P(2) | P(1) | P(2) | |
| LBOUND(A,1)の値 | 1 | 1 | 1 |
| UBOUND(A,1)の値 | 100 | 100 | 100 |
| LBOUND(A,2)の値 | 1 | 1 | 1 |
| UBOUND(A,2)の値 | 100 | 50 | 50 |
組込み関数LBOUNDとUBOUNDを利用することによって、 ローカルモデル手続中で、配列の各抽象プロセッサ上に マップされている範囲だけをアクセスするループを簡単に記述することができま す。
HPF_LOCAL手続による手続の並列起動の例は、PURE手続による並列化の例と比べると、 手続を起動する回数がはるかに少ないため、かなりの性能向上が見込めます。
次の例は、グローバルモデルのHPF手続で記述されたコードですが、 2つのサブルーチンRED1、RED2において、それぞれ、Sに対する 集計演算を行っています。
REAL S
REAL A(100),B(100)
!HPF$ DISTRIBUTE (BLOCK) :: A,B
...
CALL RED1(A,100,S)
CALL RED2(B,100,S)
END
SUBROUTINE RED1(A,100,S)
REAL A(N)
!HPF$ DISTRIBUTE A(BLOCK) ONTO P
!HPF$ INDEPENDENT,REDUCTION(S)
DO I=1,N
S = S + A(I)
ENDDO
END
SUBROUTINE RED2(B,100,S)
REAL B(N)
!HPF$ DISTRIBUTE B(BLOCK)
!HPF$ INDEPENDENT,REDUCTION(S)
DO I=1,N
S = S + B(I)
ENDDO
END
この場合、
HPFコンパイラは、
サブルーチンRED1、RED2中のループをそれぞれ配列A、Bの
マッピングに合わせて並列化して、
ローカル集計演算
を行った後、
グローバル集計演算
を行うための通信を、それぞれのループ直後に生成します。
しかし実際には、サブルーチンRED1とRED2の実行の間で、
変数Sはアクセスされないため、
グローバル集計演算
は、サブルーチンRED2のループ実行後に1度だけ行えば十分です。
HPF_LOCAL手続を利用して、以下のように記述すれば、
グローバル集計演算による通信を1度だけに押さえることが可能です。
REAL S
REAL A(100),B(100)
REAL, ALLOCATABLE :: TMP(:)
!HPF$ DISTRIBUTE (BLOCK) :: A,B,TMP
INTERFACE
EXTRINSIC(HPF_LOCAL) SUBROUTINE RED1(A,S)
REAL A(:),S(:)
!HPF$ DISTRIBUTE (BLOCK) :: A,S
END SUBROUTINE
EXTRINSIC(HPF_LOCAL) SUBROUTINE RED2(B,S)
REAL B(:),S(:)
!HPF$ DISTRIBUTE (BLOCK) :: B,S
END SUBROUTINE
END INTERFACE
...
ALLOCATE(TMP(NUMBER_OF_PROCESSORS()))
CALL RED1(A,TMP)
CALL RED2(B,TMP)
S = SUM(TMP)
DEALLOCATE(TMP)
END
EXTRINSIC(HPF_LOCAL) SUBROUTINE RED1(A,S)
REAL A(:),S(:)
DO I=1,UBOUND(A,1)
S(1) = S(1) + A(I)
ENDDO
END
EXTRINSIC(HPF_LOCAL) SUBROUTINE RED2(B,S)
REAL B(:),S(:)
DO I=1,UBOUND(B,1)
S(1) = S(1) + B(I)
ENDDO
END
上記の例では、作業配列TMPを各抽象プロセッサ上に1要素ずつ割り付けて、 ローカル集計演算 の結果を格納しておくために利用し、 グローバル集計演算 は、Fortranの組込み関数SUMにより、最後に1度だけ行っています。